PLANTEAR UN PROBLEMA DE REDES
Simplex2000â
también construye modelos de redes y diagramas de flujo de una
manera fácil e intuitiva, gracias a su poderoso motor de grafos.
Existen los siguientes tipos de
problemas de redes :
Construcción de Redes.
Problemas
de Transporte.
Problemas
de Asignación.
Problemas de
Ruta Corta.
Problemas de
Redes PERT/CPM.
Problemas de
Flujo Máximo.
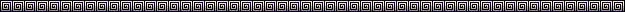
Construcción Redes de Transbordo
Se inicia con Abrir un nuevo
documento del tipo Problema de Transbordo. En seguida
aparecerá un formulario como el siguiente :
En el recuadro de la ventana se
indica el número de nodos de la red y se aplica el comando Aceptar.
Luego se van construyendo los
arcos con el botón 
;basta
seleccionar con la flecha o puntero al nodo de origen ...
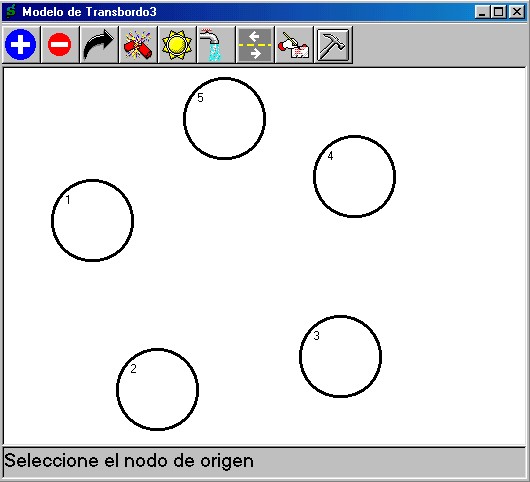
y luego seleccionar con el
puntero al nodo de destino.
Note que los nodos que tienen triángulo rojo
son nodos de entrada, y los que tienen triángulo azúl son de salida. Los
demás son nodos de transbordo.
Puede componer visualmente la
red mediante el arrastre con el botón izquierdo del mouse
sostenido hasta que los nodos queden en la posición deseada.
También puede agregar más
nodos con el botón de adición 
, o suprimir nodos con el botón de sustracción 
, o eliminar arcos
innecesarios con el botón de rompimiento 
.
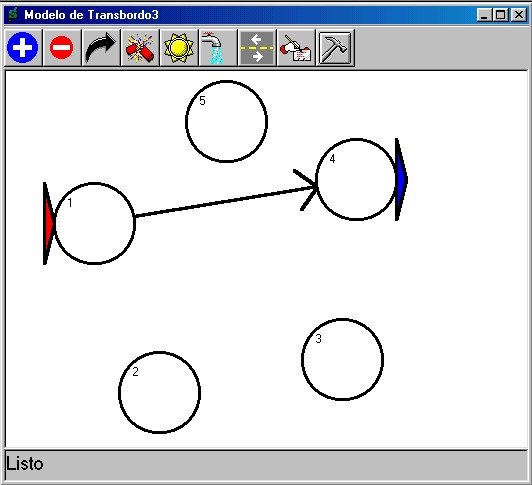
Una vez construida la red, se
asigna el valor de costo de cada arco o ruta con el botón de
suministro 
, o la
capacidad de las mismas con el botón de flujo 
. En cada caso debe
escribir el valor numérico de dicha asignación dentro del
cuadro que aparece en la parte superior derecha del formulario:
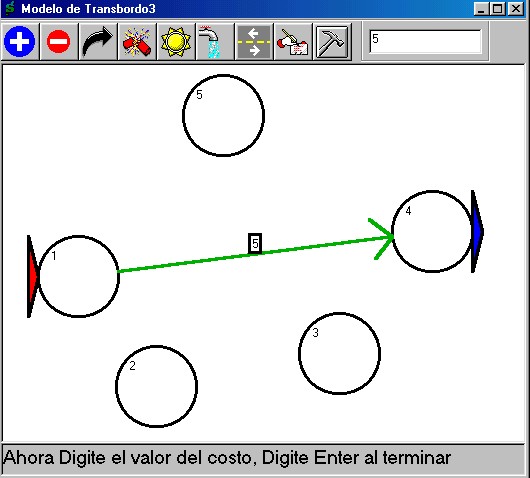
Note que algunos costos pueden
quedar escritos hacia abajo, esto se corrige al adecuar
nuevamente los arcos de izquierda a derecha; también se puede
modificar el tamaño de los números para una mejor visualización.
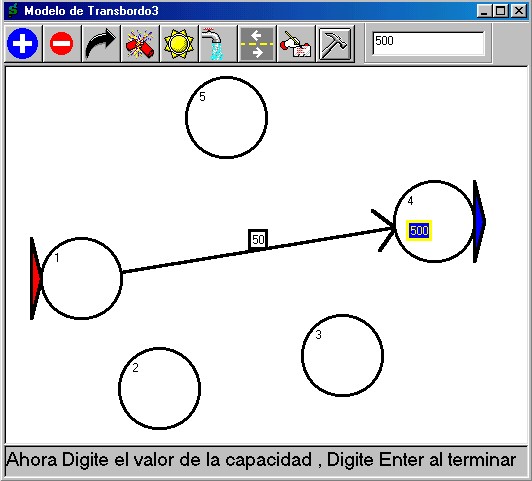
Ahora, se asignan los valores
numéricos en los nodos de entrada, de transbordo o de salida según
la capacidad de cada uno de ellos; basta aplicar el botón de oro
, se hace de la misma
manera tal como se hizo para los costos de los arcos:
Por último, al hacer clic en
el botón martillo decisorio 
se obtiene una solución al problema. Simplex2000Ò
crea y soluciona automáticamente el modelo de Programación
Lineal correspondiente y en el gráfico se dibujarán la rutas óptimas
coloreadas de azul:
Regresar al indice de redes.
Regresar al contenido principal.
Regresar al menu de tutoriales.
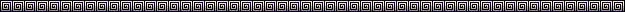
Problemas de Transporte
En esta modalidad
de problemas la Red estará constituida por nodos de oferta y de
demanda. Se empieza con abrir un nuevo documento de tipo Problema
de Transporte.; en seguida aparecerá un formulario como el
siguiente :
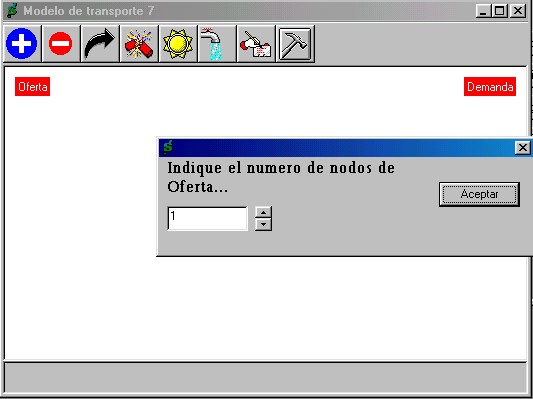
El formulario
solicita que se escriba dentro del recuadro el número de nodos
de oferta, se aplique Aceptar ; luego solicita el
número de nodos de demanda.
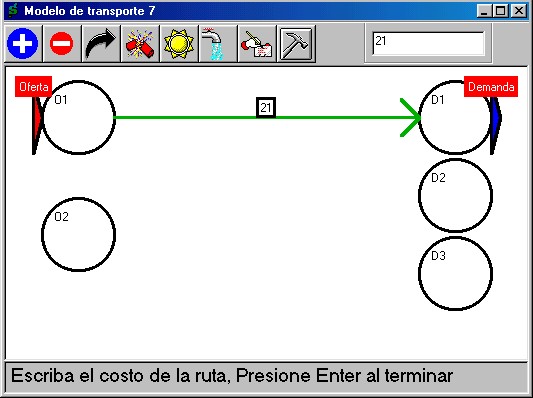
Posteriormente el
modelo requiere la construcción de cada ruta, por ello en el
recuadro se hace la pregunta del arco correspondiente. En caso
negativo, por defecto no se definirá la variable de doble índice
en referencia.
Sobre cada arco
construido se hace clic para asignarle el costo correspondiente.
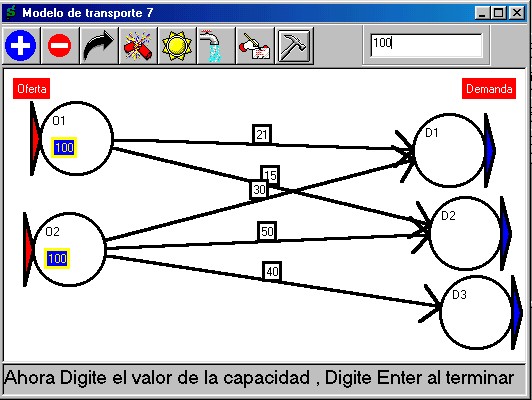
Luego de asignar todos los
cosotos sobre los arcos, el programa solicitará el valor numérico
para los nodos de oferta y el valor para los nodos de demanda:
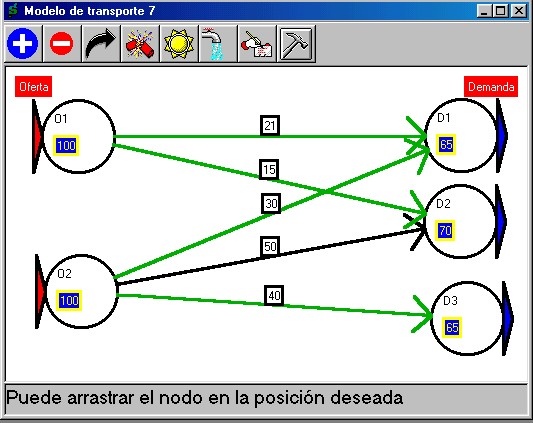
Por último, al hacer clic en
el botón se obtiene
una solución al problema. Simplex2000Ò crea y
soluciona el modelo de Prog. Lin. por Ud., así que sobre el
grafico aparecerán los arcos óptimos coloreadas de verde.
El modelo de Prog.
Lin. consistente en minimizar los costos de transporte cumpliendo
las limitaciones de las ofertas y las cotas de las demandas es
planteado y solucionado automáticamente por el programa y puede
ser visto desde la ventana del Mapa de solución. Existen modelos
de Transporte diferentes al ejemplo anterior en el que están
desequilibrados los totales de las ofertas y de las demandas, en
tales casos aparecerán las holguras y excedentes respectivos.
Regresar al indice de redes.
Regresar al contenido principal.
Regresar al menu de tutoriales.
Problemas de Asignación
Al abrir un nuevo documento del
tipo Problema de asignación el ingreso de datos se hace
sobre el mismo grafo; allí se pregunta por el número de agentes
a los cuales se les asignarán las tareas y el número de
trabajos o tareas que ellos pueden ejecutar. Acto seguido se
dispone sobre cada arco el coeficiente de tiempo (en el caso de
minimizar el tiempo en las jornadas de trabajo ), o de eficiencia
(si el caso es de maximizar, los índices de récord en
productividad ), dependientes de las características inherentes
a este tipo de problemas. Por ejemplo, el siguiente grafo muestra
varios tiempos que emplean tres agentes para realizar tres tipos
de trabajo :
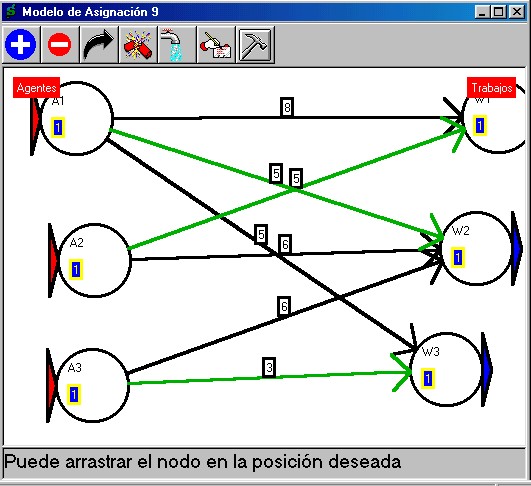
Luego de aplicar
el símbolo de martillo , se obtiene la solución resaltada con las flechas
de color verde interpretadas así:
El agente 1 hará
el trabajo 2 en 5 horas, el agente 2 hará el trabajo 1 en 5
horas y el agente 3 hará el trabajo 3 en 3 horas. El modelo de
Prog. Lin. consistente en minimizar las horas es planteado y
solucionado automáticamente por el programa y puede ser visto
desde la ventana del Mapa de solución.
Regresar al indice de redes.
Regresar al contenido principal.
Regresar al menu de tutoriales.
Problemas de Ruta Corta.
Al abrir un nuevo documento de
tipo Problema de Ruta Corta., se indicarán los arcos
conectados entre los nodos de actividad y los tiempos de ejecución
de modo secuencial. Se pretende determinar la ruta que totalice
los mínimos tiempos desde el nodo inicial hasta el nodo final.
Luego de aplicar el botón martillo , se obtiene la solución resaltada con
las flechas de color verde.
El modelo de Prog.
Lin. consistente en minimizar las horas es planteado y
solucionado automáticamente por el programa y puede ser visto
desde la ventana del Mapa de solución.
Regresar al indice de redes.
Regresar al contenido principal.
Regresar al menu de tutoriales.
Problemas de Redes PERT/CPM
Al abrir un nuevo documento de
tipo Problema de Red PERT/CPM. se indicarán los
arcos conectados entre los nodos de actividad y los tiempos de
ejecución de modo secuencial. Se pretende determinar la ruta que
totalice el máximo tiempo desde el nodo inicial hasta el nodo
final. Luego de aplicar el botón martillo , se obtiene la solución
resaltada con las flechas de color verde.
El modelo de Prog. Lin.
consistente en maximizar los tiempos y determinar la Ruta Crítica
necesaria en la Revisión y Evaluación Técnica del Proyecto de
actividades en general, se plantea y soluciona automáticamente
por el programa el cual puede ser visto desde la ventana del Mapa
de solución.
Regresar al indice de redes.
Regresar al contenido principal.
Regresar al menu de tutoriales.
Problemas de Flujo Máximo
Al abrir un nuevo documento de
tipo Problema de Flujo Máximo. se indicarán los arcos
conectados entre las estaciones o nodos de bifurcación y las
capacidades secuenciales de los arcos. Se pretende maximizar el
Flujo que se puede hacer pasar a través de toda la red desde el
nodo inicial hasta el nodo final.
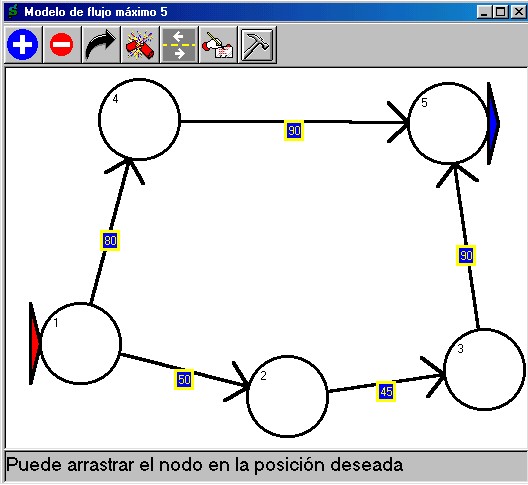
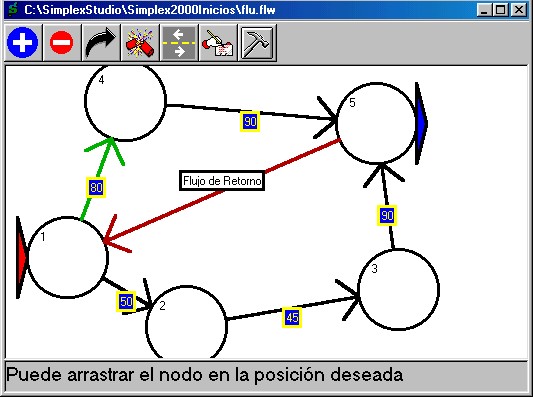
Es importante señalar que en
la construcción de este tipo de redes, aparece un arco de
retorno por efecto de una variable artificial que ayuda en la
solución del modelo; éste arco no lo realiza el usuario sino
que aparece al final del proceso.
He aquí, la tabla final del
modelo de Programación Lineal planteado automáticamente por el
programa a partir del gráfico de Red:
| ITERACION Nº 7 |
| Variable Entrante : X3:5 |
Variable Saliente : H8 |
| DESIGUALDAD |
BASICAS |
X5:1 |
X1:2 |
X1:4 |
X2:3 |
X3:5 |
X4:5 |
H6 |
H7 |
H8 |
H9 |
H10 |
COTA |
| = |
X5:1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
125 |
| = |
X1:2 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
45 |
| = |
X2:3 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
45 |
| = |
X1:4 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
80 |
| = |
H6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
-1 |
0 |
0 |
5 |
| <= |
X4:5 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
80 |
| <= |
X3:5 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
45 |
| <= |
H9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
45 |
| <= |
H10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
10 |
| MAX |
Z:= |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
125 |
Luego de aplicar el botón
martillo , se
obtiene la solución consistente en un valor numérico de flujo máximo
el cual puede obtenerse desde el mapa de solución.
*** SOLUCION PARA VARIABLES DE DECISION BASICAS ***
| Variable |
Variación |
| X5:1=125 |
0 <= C1 = 1 <=Sin Cota Superior |
| Z Mínimo = 0 |
Sin Z Máximo |
| X1:2=45 |
-1 <= C2 = 0 <=Sin Cota Superior |
| Z Mínimo = 80 |
Sin Z Máximo |
| X1:4=80 |
-1 <= C3 = 0 <=Sin Cota Superior |
| Z Mínimo = 45 |
Sin Z Máximo |
| X2:3=45 |
-1 <= C4 = 0 <=Sin Cota Superior |
| Z Mínimo = 80 |
Sin Z Máximo |
| X3:5=45 |
-1 <= C5 = 0 <=Sin Cota Superior |
| Z Mínimo = 80 |
Sin Z Máximo |
| X4:5=80 |
-1 <= C6 = 0 <=Sin Cota Superior |
| Z Mínimo = 45 |
Sin Z Máximo |
*** SOLUCION PARA COTAS DE RESTRICCION BASICAS ***
| Holgura o Excedente |
Variación |
| H6=5 |
45 <= B1 = 50<=Sin Cota Superior |
| Z Mínimo = 0 |
Sin Z Máximo |
| H9=45 |
45 <= B4 = 90<=Sin Cota Superior |
| Z Mínimo = 0 |
Sin Z Máximo |
| H10=10 |
80 <= B5 = 90<=Sin Cota Superior |
| Z Mínimo = 0 |
Sin Z Máximo |
Note que las
variables resultan con doble índice para indicar el nodo inicial
y el nodo final que conectan; las holguras corresponden a los
valores de capacidad sobrantes. El flujo máximo que puede
hacerse pasar a través de la red es de 125.
Regresar al indice de redes.
Regresar al contenido principal.
Regresar al menu de tutoriales.