Lógica
Modal
O primeiro sistema de lógica modal foi
apresentado por Lewis em 1918 e posteriormente em
forma definitiva em 32 com a colaboração de
Cooper H. Langford em "Symbolic Logic".
Minuciosamente construída, a lógica modal
estuda a razão que envolve e usa das expres-
sões 'necessariamente' e 'possivelmente'.
Entretando, o termo 'lógica modal' pode ser
usado mais amplamente cobrindo uma família de
lógicas com regras similares e uma
variedade de símbolos diferentes.
Segue uma tabela com o
melhor conhecimento destas lógicas:
| Lógica |
Símbolos |
Expressões
Simbolizadas |
| Lógica Modal |
 |
É necessário
que... |
| |
 |
É possível que... |
| Lógica "Deontic" |
O |
É obrigatório
que... |
| |
P |
É permitido que... |
| |
F |
É proibido que... |
| Lógica Temporal |
G |
Sempre será o caso
que... |
| |
F |
Será o caso que... |
| |
H |
Sempre foi o caso
que... |
| |
P |
Era o caso que... |
| Lógica "Doxastic" |
Bx |
x acredita que... |
As mais
familiares lógicas da família das modais foram
contruídas de um lógica "weak"
chamada K (depois Saul Kripke). A lógica modal,
preocupa-se com necessidade e possi- bilidade.
Uma variedade de sistemas diferentes, podem ser
desenvolvidos para tais lógicas usando a K como
base. Os símbolos de K incluem "~" para
"negação", "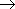 "
para "se...então", e " "
para "se...então", e " "
para o operador modal "é necessário
que".(Os conectivos "&,^",
" "
para o operador modal "é necessário
que".(Os conectivos "&,^",
" ", e " ", e " " podemser definidos como "~" e
" " podemser definidos como "~" e
"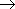 " como é usado na lógica
proposicional.) K resulta da adição das
seguintes regras aos princípios da lógica
proposicional: " como é usado na lógica
proposicional.) K resulta da adição das
seguintes regras aos princípios da lógica
proposicional:
Regra da necessidade: Se A é um teorema de K,
então é  A. A.
Distribuindo o Axioma:  (A (A 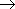 B)
B) 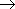 ( ( A A 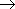
 B). B).
(Nesses princípios usamos 'A' e 'B', como
metavariáveis variando em cima da fórmula da
linguagem.)De acordo com a Regra de Necessidade,
alguns teoremas de lógica são ne-
cessários. A distribuição do axioma diz que se
é necessário que A então B, então é ne-
cessário A então é necessário B.
O operador  (para possibilidade),
pode ser definido de (para possibilidade),
pode ser definido de  admitindo admitindo  A = ~
A = ~ ~A. No K ~A. No K
os operadores  e e  comportam-se muito bem como os quantificadores
comportam-se muito bem como os quantificadores  (todos) e
(todos) e 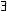
(alguns). Por exemplo, a definição de  de
de  espelham a equivalência de espelham a equivalência de  xA com xA com
~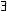 x ~A na lógica
predicativa. Além disso, x ~A na lógica
predicativa. Além disso,  (A&B) víncula (A&B) víncula  A& A& B e vice
versa; enquanto B e vice
versa; enquanto
 A A  B vincula B vincula  (A (A B), mas não
vice versa. Isto reflete os padrões exibidos
pelos quanti- B), mas não
vice versa. Isto reflete os padrões exibidos
pelos quanti-
ficadores universais:  x(A&B)
vincula x(A&B)
vincula  xA& xA& xB e vice versa, enquanto xB e vice versa, enquanto  xA xA  xB reflete xB reflete
 x(A x(A B) mas não
vice versa. Similar comparação entre B) mas não
vice versa. Similar comparação entre  e
e 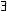 pode ser vista. pode ser vista.
Para voltar a página
principal, clique aqui.
|