4.2  Graphing Linear Equations in Two Variables

Mrs. Agriesti's Algebra

Goal:  To learn to graph linear equations using a table of values.

Monday we learned how to graph equations that had only one variable, either x or y (x = some number or y = some number).  Our graphs were either horizontal or vertical lines.  Today we will graph equations with both x and y and we will get lines that have a slant (or slope).

We are going to use a table of values to plot a few points and sketch our line.  To construct a table of values, I want you to choose at least three x values spread evenly apart.  Most of the time I recommend using x = -3, 0, & 3.  If the coefficient of x in the equation is a fraction then I recommend using a multiple of the denominator of that fraction instead.  For example in the equation y = (1/2)x + 3, I would use a multiples of 2 such as -4, 0, & 4.

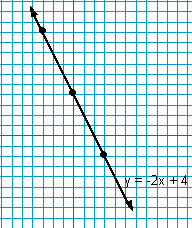
Example 1:     Sketch the graph of y = -2x + 4.

First construct your table of values by drawing your table with three columns; x, y, and y = -2x+ 4. 

Fill in the x column with the values you chose ( I chose -3, 0, and 3). 

Find the corresponding y-values by substituting each x-value into the equation and solving.  Make sure to show each and every step.  Put your answers in the y-column. 

Now that the table is complete plot the points for the solutions you found.  For this example the points are  (-3,10), (0,4), and (3,-2). 

The points should line up.  If they don't you need to find your error. 

If they line up, use a straight-edge to draw a line through them. 

Make sure to add arrows to the line and label it.

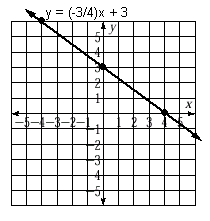
Example 2:     Sketch the graph of y = (-3/4)x + 3.

First construct your table of values by drawing your table with three columns; x, y, and y = (-3/4)x + 3. 

Fill in the x column with the values you chose ( I chose -4, 0, & 4 because they are multiples of the denominator of the coefficient of x). 

Find the corresponding y-values by substituting each x-value into the equation and solving.  Make sure to show each and every step.  Put your answers in the y-column. 

Now that the table is complete plot the points for the solutions you found.  For this example the points are  (-4,6), (0,3), and (4,0). 

The points should line up.  If they don't you need to find your error. 

If they line up, use a straight-edge to draw a line through them. 

Make sure to add arrows to the line and label it.