You can graph variations on basic functions using transformations to shift, reflect and reshape the basic equation. Study the following representation:

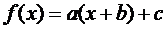
Vertical Shift:
The element "c" results in a vertical shift. If c is positive, the basic function shifts c units up. If c is negative, the basic function shifts c units down. Notice that "c" occurs outside of the basic function.

Horizontal Shift:
The element "b" results in a horizontal shift. If b is positive, the basic function shifts b units to the left. If b is negative, the basic function shifts b units to the right. Notice that "b" occurs inside of the basic function.

Vertical Stretch or Compression:
The element "a" results in a vertical stretch or compression. When a is greater than 1 the basic function stretches vertically. In other words, the graph gets thinner. A value of less than 1 will cause the basic function to compress vertically, or become wider.

Reflection about the x and y axis:
If "x" is negative, the basic graph reflects about the y-axis. If "f(x)" is negative, the basic graph reflects about the x-axis.

Functions often contain more than one characteristic that makes them different from their basic form. We can "transform" these functions with the techniques described above, used together. For instance, the basic square function can have vertical stretch, reflection, horizontal shift and vertical shift applied to create a completely transformed square function.

The basic identity function can also have multiple transformations applied to create a new identity function.