Aims and Objectives
We begin with a coupled map lattice designed to model insect population dynamics which, while undergoing diverging oscillations for zero coupling and almost all initial conditions, displays long-term non-homogeneous behaviour on the lattice for small positive values of the coupling parameter, notably spiral waves and spatial chaos. We would like to understand how this can be.However, the biological model's local map is highly asymmetric and defined on an infinite domain, so to understand the mechanisms at work we spend the greater part of the thesis investigating a more mathematically friendly system which is defined on the closed unit disc and commutes with rotations, while at the same time bearing more than a passing resemblance to the biological model and displaying the same sorts of behaviour when coupled in a lattice.
We prove the existence of persistent one-dimensional waves and regular spiral configurations for the friendly equations, use circulant matrices results to prove stability of one-dimensional waves for small non-zero coupling and provide numerical evidence for the stability of the spirals. We also give an in-depth account of the special attractors observed on the 2x2 lattice and the bifurcations responsible for their creation, which, while not strictly relevant to the main problem, form an integral part of our system's full dynamics.
By the end we will have completed a thorough investigation into our specially constructed `friendly' dynamical system, and while we are unable to carry the results across directly to the biological model there seems little doubt that the processes at work in the one must be analogous to the less symmetric processes taking place in the other. Our friendly set of equations does not appear to be at all limited in the richness of its behaviour by its simplicity - rather it seems that asymmetries are an uunnecessary complication when trying to understand such observed spatial dynamics.
Lattice simulations for a range of variations on the friendly local map display similar patterns, suggesting that what we may be looking at is just one representative of a much larger family of dynamical systems, and we hope that the properties of the system studied here will be useful in understanding the dynamics of its relatives.
Chapter 2 -
We summarise the behaviour of the two lattices for a range of parameter values
and lattice sizes, and note the similarities. This is where we leave the
difficult biological model equations. The rest of the thesis will take the form
of an investigation into our simpler system. The reader is left to judge how
much of what we learn can be seen as relevant to the biological model.
Chapter 3 -
Restricting attention to the friendlier of the two systems, we begin by
investigating the rich variety of behaviours observed in the 2x2 lattice. For
small coupling orbits accumulate on a torus, and we display numerous trajectory
plots and infer from them the bifurcations which lead to the formation of
various different kinds of attractor, among them fixed points which do not
correspond to a homogeneous lattice, and closed orbits which undergo
length-doubling bifurcations as the torus breaks up.
Chapter 4 -
We then move on to larger lattices and make a definition of what it means to
have a spiral centre present. We describe a number of symmetries preserved by
the dynamics and the invariant linear subspaces which they generate. We also
look at the series of bifurcations at the origin which take place as the
coupling parameter is varied, which we will later associate with the creation
of at least partial surfaces of points whose distances from the origin are
unchanged by a single iteration of the dynamics, and which include
one-dimensional lattice waves and regularly distributed spiral structures.
Chapter 5 -
We limit our attention to one-dimensional patterns on the lattice for non-zero
coupling. Using properties of circulant matrices, we prove that the homogeneous
lattice fixed points are always stable to perturbations, the checkerboard and
one-dimensional waves of spatial periods 2, 3 and 4 always unstable in at least
one direction (the 4 case provided coupling is small), and waves of spatial
period greater than or equal to 5, and equal to the lattice size in the
direction of travel, stable for small coupling and small values of the local
map parameter.
Chapter 6 -
Finally we return to our investigation of regular spirals on an even-sized
lattice and argue that in suitable parameter ranges such configurations exist
as fixed points (up to uniform rotation of all lattice sites) close to their
corresponding creation bifurcations at the origin. We show that regular
configurations of four spiral centres on 2x2 and 4x4 lattices are unstable for
small coupling, but numerical computations of eigenvalues for the 6x6 and 8x8
cases indicate that larger spirals are in fact stable in certain regions of
parameter space.
Chapter 7 -
We take stock of what we have learnt, say a few additional words on the
biological model and give a wish-list for future research on the more friendly
system. We also mention other works which expand more fully on the topics of
coupled map lattices, the Nicholson-Bailey system and spiral waves in
continuous media.
Appendices -
Here we work through the algorithm for inverting the local map of the more
friendly system, should it be required for future research (perhaps to compute
stable manifolds of saddle points), provide an alternative proof of the
stability of one-dimensional lattice waves of length 8, and give a rough idea
of the types of dominant behaviour observed on square lattices of various sizes
besides the 30x30 case discussed in the main text. Finally we display a number
of lattices generated by variations on the local map which we have been
studying, and after the bibliography the reader will find a larger version of
the 2x2 lattice bifurcation diagram discussed in Chapter 3.
The random lattice simulations were performed on the C program
thing.c which outputs an ASCII representation to both the
screen and a plain text file, which may then be fed into the QBasic program
graphic.bas to generate an image that may be captured
by appropriate screen capture software and converted into animated GIF format.
The regularly distributed spirals were created using
regular.c.
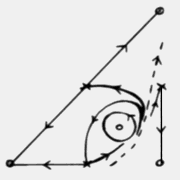
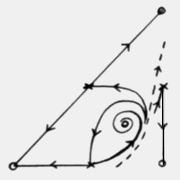
The C program's screen output shows, in addition to each site's current
quadrant, the location of every clockwise and anticlockwise spiral centre, and
the modulus at each site. Local minima of the moduli coincide with spiral
centres, as do the points on the lattice where all four colours come
together.
A 100x100 lattice bitmap can be generated directly from Unix by using the
program bitmap.c, provided the bare bones bitmap
thing.bmp is replaced before each iteration.
For screen output only, take any of these C programs and delete all lines
containing the fprintf command.
If you have any questions, please e-mail
martinmcvay@yahoo.co.uk. Thank
you!
A Guide to this Thesis
Chapter 1 -
We define two dynamical systems, both two-dimensional coupled map lattices. One
describes an established biological model, the other a simpler, friendlier
system which displays similar behaviour in computer simulations. Both systems
can be decomposed into the local map and a coupling matrix which acts on the
vector of ordered lattice variables. The coupling map is common to both
systems, and usually takes the form of a block circulant matrix with circulant
blocks. The properties of such matrices, which will be critical to many of the
proofs in this thesis regarding the friendly system, are described, as are the
orbits of the two local maps.Animated GIFs
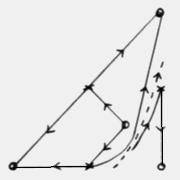
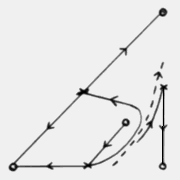
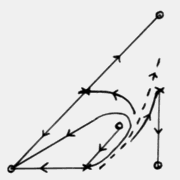
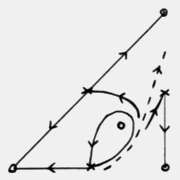
We look at the behaviour of a two-dimensional coupled map lattice where each
site is associated with a complex number lying in the closed unit disc. We vary
two parameters, δ, which affects the local map, and ε, the
diffusive coupling strength. Initial conditions are random unless otherwise
stated. The local map is described in detail in Chapter 1.


















































The 2x2 Lattice Bifurcations
Click here and
here to see the special bifurcation sequences
described in Chapter 3 for the 2x2 lattice.