Home Up Search

Mean Value Theorem Of Integrals
Calculus I
Calculus II
Chemistry
Physics
Oceanography

By Rick Stoll          

 Calc I

 

[Under Construction]

 

 

 

Let f (x) be continuous on [a, b]. Set

 

F(x) = $\displaystyle \int_{a}^{x}$f (t)dt  .

 

The Fundamental Theorem of Calculus implies F '(x) = f (x). The Mean Value Theorem implies the existence of c $ \in$ (a, b) such that

 

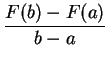$\displaystyle {\frac{F(b) - F(a)}{b-a}}$ = F '(c),    or equivalently    F(b) - F(a) = F '(c)$\displaystyle \Big($b - a$\displaystyle \Big)$

 

which implies

 

$\displaystyle \int_{a}^{b}$f (t)dt = f (c)$\displaystyle \Big($b - a$\displaystyle \Big)$  .

 

This is known as the First Mean Value Theorem for Integrals. The point f (c) is called the average value of f (x) on [a, b].

As the name "First Mean Value Theorem" seems to imply, there is also a Second Mean Value Theorem for Integrals:

Second Mean Value Theorem for Integrals. Let f (x) and g(x) be continuous on [a, b]. Assume that g(x) is positive, i.e. g(x) $ \geq$ 0 for any x $ \in$ [a, b]. Then there exists c $ \in$ (a, b) such that

 

$\displaystyle \int_{a}^{b}$f (t)g(t)dt = f (c)$\displaystyle \int_{a}^{b}$g(t)dt  .

 

The number f (c) is called the g(x)-weighted average of f (x) on the interval [a, b].

As an application one may define the Center of Mass of one-dimensional non-homogeneous objects such as a metal rod. If the object is homogeneous and lying on the x-axis from x = a to x = b, then its center of mass is simply the midpoint

 

$\displaystyle {\frac{a+b}{2}}$   .

 

If, on the other hand, the object is not homogeneous with $ \lambda$(x) being the density function, then the total mass M is

 

M = $\displaystyle \int_{a}^{b}$$\displaystyle \lambda$(x)dx  .

 

The density-weighted average xc is defined by

 

$\displaystyle \int_{a}^{b}$x$\displaystyle \lambda$(x)dx = xc$\displaystyle \int_{a}^{b}$$\displaystyle \lambda$(x)dx = xcM,

 

or equivalently

 

xc = $\displaystyle {\frac{1}{M}}$$\displaystyle \int_{a}^{b}$x$\displaystyle \lambda$(x)dx  .

 

The point xc is the center of mass of the object.

Example. A rod of length L is placed on the x-axis from x = 0 to x = L. Assume that the density $ \lambda$(x) of the rod is proportional to the distance from the x = 0 endpoint of the rod. Let us find the total mass M and the center of mass xc of the rod. We have $ \lambda$(x) = kx, for some constant k > 0. We have

 

M = $\displaystyle \int_{0}^{L}$$\displaystyle \lambda$(x)dx = $\displaystyle \int_{0}^{L}$kxdx = k$\displaystyle {\frac{L^2}{2}}$ = $\displaystyle {\frac{kL^2}{2}}$

 

and

 

xc = $\displaystyle {\frac{1}{M}}$$\displaystyle \int_{0}^{L}$x$\displaystyle \lambda$(x)dx = $\displaystyle {\frac{1}{M}}$$\displaystyle \int_{0}^{L}$kx2dx = $\displaystyle {\frac{1}{M}}$k$\displaystyle {\frac{L^3}{3}}$ = $\displaystyle {\textstyle\frac{2}{3}}$L  .

 

If the rod was homogeneous, then the center of mass would be at the midpoint of the rod. Now it is closer to the endpoint x = L. This is not surprising since there is more mass at this end.

Exercise 1. Find the average value of

 

f (x) = sec2(x)

 

for x $ \in$ [0,$ \pi$/4].

 

 

 

 

 

Exercise 2. Find the average value of

 

f (x) = $\displaystyle \sqrt{x}$

 

for x $ \in$ [0, 4].

 

 

 

 

 

Exercise 3. Assume that f (x) be continuous and increasing on [a, b]. Compare

 

f (a)(b - a)    and    $\displaystyle \int_{a}^{b}$f (x)dx  .

 

 

 

 

 

 

Send mail to m_engineer2002@netzero.com with questions or comments about this web site.
Copyright © 2001 Math Depot
Last modified: April 30, 2001