Home Up Search

Continuity
Calculus I
Calculus II
Chemistry
Physics
Oceanography

By Rick Stoll          

 Calc I

 

[Under Construction]

 

 

 

We have seen that any polynomial function P(x) satisfies:

 

\begin{displaymath}\lim_{x \rightarrow a} P(x) = P(a)\;\end{displaymath}

 

for all real numbers a. This property is known as continuity.

Definition. Let f(x) be a function defined on an interval around a. We say that f(x) is continuous at a iff

 

\begin{displaymath}\lim_{x \rightarrow a} f(x) = f(a)\;.\end{displaymath}

 

Otherwise, we say that f(x) is discontinuous at a.

Note that the continuity of f(x) at a means two things:

(i)
$\displaystyle \lim_{x \rightarrow a} f(x)$ exists,
(ii)
and this limit is f(a).
So to be discontinuous at a, means
(i)
$\displaystyle \lim_{x \rightarrow a} f(x)$ does not exist,
(ii)
or if $\displaystyle \lim_{x \rightarrow a} f(x)$ exists, then this limit is not equal to f(a).

Basic properties of limits imply the following:

Theorem. If f(x) and g(x) are continuous at a. Then

(1)
f(x) + g(x) is continuous at a;
(2)
$\alpha f(x)$ is continuous at a, where $\alpha$ is an arbitrary number;
(3)
$f(x)\;g(x)$ is continuous at a;
(4)
$\displaystyle \frac{f(x)}{g(x)}$ is continuous at a, provided $g(a) \neq 0$;
(5)
If f(x) is positive, i.e. $f(x) \geq 0$, then $\sqrt{f(x)}$ is continuous at a;
(6)
If f(x) is continuous at a and g(x) is continuous at g(a), then their composition $g \circ f(x)$ is continuous at a.

Remark. Many functions are not defined on open intervals. In this case, we can talk about one-sided continuity. Indeed, f(x) is said to be continuous from the left at a iff

 

\begin{displaymath}\lim_{x \rightarrow a-} f(x) = f(a)\;,\end{displaymath}

 

and f(x) is said to be continuous from the right at a iff

 

\begin{displaymath}\lim_{x \rightarrow a+} f(x) = f(a)\;.\end{displaymath}

 

Example. The function $f(x) = \sqrt{x}$ is defined for $x \geq 0$. So we can not talk about left-continuity of f(x) at 0. But since

 

\begin{displaymath}\lim_{x \rightarrow 0+} \sqrt{x} = 0\;,\end{displaymath}

 

we conclude that f(x) is right-continuous at 0.

This concept is also important for step-functions.

Example. Consider the function

 

\begin{displaymath}f(x) = \left\{ \begin{array}{rll} x^3 + 2& \mbox{if $x < 2$}\... ...x = 2$}\\ x^2 + 6 & \mbox{if $x > 2$}\;.\\ \end{array}\right.\end{displaymath}

 

The details are left to the reader to see

 

\begin{displaymath}\lim_{x \rightarrow 2-} f(x) = \lim_{x \rightarrow 2-} x^3 + 2 = 10,\end{displaymath}

 

and

 

\begin{displaymath}\lim_{x \rightarrow 2+} f(x) = \lim_{x \rightarrow 2+} x^2 + 6 = 10.\end{displaymath}

 

So we have

 

\begin{displaymath}\lim_{x \rightarrow 2} f(x) = 10.\end{displaymath}

 

Since f(2) = 5, then f(x) is not continuous at 2.

 

 

 

Exercise 1. Find A which makes the function

 

\begin{displaymath}f(x) = \left\{ \begin{array}{rll} x^2 - 2& \mbox{if $x < 1$}\\ A x - 4 & \mbox{if $1 \leq x$}\\ \end{array}\right.\end{displaymath}

 

continuous at x=1.

 

 

 

 

 

 

 

Definition. For a function f(x) defined on a set S, we say that f(x) is continuous on S iff f(x) is continuous for all $a \in S$.

Example. We have seen that polynomial functions are continuous on the entire set of real numbers. The same result holds for the trigonometric functions $\sin(x)$ and $\cos(x)$.

The following two exercises discuss a type of functions hard to visualize. But still one can study their continuity properties.

 

Exercise 2. Discuss the continuity of

 

\begin{displaymath}f(x) = \left\{ \begin{array}{lll} 1 &\mbox{if $x$ is rational}\\ 0 &\mbox{if $x$ is irrational.}\\ \end{array}\right.\end{displaymath}

 

 

 

 

 

 

 

 

 

Exercise 3. Let us modify the previous function: Discuss the continuity of

 

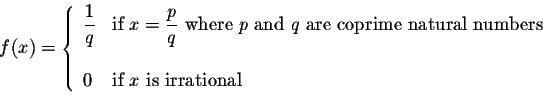
\begin{displaymath}f(x) = \left\{ \begin{array}{lll} \displaystyle \frac{1}{q} &... ...s}\\ &\\ 0 &\mbox{if $x$ is irrational}\\ \end{array}\right.\end{displaymath}

 

for $x \in (0,1)$. (Two natural numbers p and q are coprime, if their greatest common divisor equals 1.)

 

Back to the top of page

 

 

Send mail to m_engineer2002@netzero.com with questions or comments about this web site.
Copyright © 2001 Math Depot
Last modified: April 30, 2001