Home Up Search

Intro to limit definitions
Calculus I
Calculus II
Chemistry
Physics
Oceanography

By Rick Stoll          

 Calc I

 

[Under Construction]

 

 

 

The concept of a limit is fundamental to Calculus. In fact, Calculus without limits is like Romeo without Juliet. It is at the heart of so many Calculus concepts like the derivative, the integral, etc. So what is a limit?

Maybe the best example to illustrate limits is through average and instantaneous speeds: Let us assume you are traveling from point A to point B while passing through point C. Then we know how to compute the average speed from A to B: it is simply the ratio between the distance from A to B and the time it takes to travel from A to B. Though we know how to compute the average speed this has no real physical meaning.

Indeed, let us suppose that a policeman is standing at point C checking for speeders going through C. Then the policeman does not care about the average speed. He only cares about the speed that you see on the speedometer, the one that the car actually has when crossing C. That one is real.

How do we compute this "instantaneous speed"? That's not easy at all! Naturally one way to do this is to compute the average speed from C to points close to C. In this case, the distance between these points and C is very small as well as the time taken to travel from them to C. Then we look at the ratio: Do these average speeds over small distances get close to a certain value? If so, that value should be called be the instantaneous speed at C. In fact, this is exactly how the policeman's radar computes the driver's speed!

Let us express this more mathematically. If s(t) is a function that determines the position of the moving object, and assume that at time t0, the moving object is at C. At $t_0 + \Delta t$, we are at a point close to C. Then the average speed between these two points is

 

\begin{displaymath}\frac{s(t_0 + \Delta t) - s(t_0)}{\Delta t}\cdot\end{displaymath}

 

Then we study these numbers when $\Delta t$ gets smaller and smaller. This is exactly the idea behind the concept of limit. We will write

 

\begin{displaymath}\lim_{\Delta \rightarrow 0} \frac{s(t_0 + \Delta t) - s(t_0)}{\Delta t}\end{displaymath}

 

to indicate the instantaneous speed at C.

Before we state the formal definition of the limit, let us consider the function $f(x) = \displaystyle \frac{\sin(x)}{x}$. What is

 

\begin{displaymath}\lim_{x \rightarrow 0}\frac{\sin(x)}{x}?\end{displaymath}

 

Clearly this function makes sense as long as the input is not equal to 0. In other words, we can take as an input any number close enough to 0, but not 0 itself.

 

It is clear by looking at the outputs that, when x gets close to 0, $\displaystyle \frac{\sin(x)}{x}$ is getting close to 1. We say that $\displaystyle \frac{\sin(x)}{x}$ has a limit of 1 when x goes to 0 and write

 

\begin{displaymath}\lim_{ x \rightarrow 0} \frac{\sin(x)}{x} = 1\;.\end{displaymath}

 

You have to be very careful when you use calculators not to jump to conclusions too quickly. Quantities may be getting close to each other up to a certain point but then they may move further away from each other again. This happens frequently when dealing with chaotic systems, for example. Most of the calculators do computations up to nine digits or so. So two numbers with the same nine decimals are equal (according to the calculator). Be aware of the dangers from these shortcomings of calculating devices! But in the above statement, we mean that $\displaystyle \frac{\sin(x)}{x}$ is getting as close to 1 as we wish. Of course, if you want to get close up to 75 decimals then you will have to consider inputs x extremely close to 0. In other words, for a given error $\varepsilon > 0$, then if x is close enough to 0, we will have $\displaystyle \frac{\sin(x)}{x}$ is getting close to 1 up to $\varepsilon $, or equivalently

 

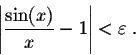
\begin{displaymath}\left\vert\frac{\sin(x)}{x} - 1\right\vert < \varepsilon\;.\end{displaymath}

 

How do we express: "x very close to 0"? Simply by saying that there exists 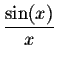$\delta > 0$ such that $\vert x - 0\vert < \delta$. Of course, as we said before, if $\varepsilon $ is very small, then $\delta$ will usually have to be very small. In other words, $\delta$, which controls how close we should be to 0, depends on how fast the function $\displaystyle \frac{\sin(x)}{x}$ is getting closer to 1, and on the size of $\varepsilon $. Putting these ideas together, one can come up with the following formal definition.

Definition of limit. Let f(x) be a function defined around a point c, maybe not at c itself. We have

 

\begin{displaymath}\lim_{ x \rightarrow c} f(x) = L\end{displaymath}

 

iff for any $\varepsilon > 0$, there exists $\delta > 0$ such that

 

\begin{displaymath}\mbox{if}\;\; \vert x - c\vert < \delta \;\;\ \mbox{then}\;\; \vert f(x) - L\vert < \varepsilon\;.\end{displaymath}

 

The number L is called the limit of f(x) when x goes to c.

Sometimes the function is not defined around the point c but only to the left or right of c. Then we have the concepts of left-limit and right-limits at c.

(i)
L is the left-limit of f(x) at c iff for any $\varepsilon > 0$, there exists $\delta > 0$ such that

 

\begin{displaymath}\mbox{if}\;\; c -\delta<x < c \;\;\ \mbox{then}\;\; \vert f(x) - L\vert < \varepsilon\end{displaymath}

 

and write $L = \displaystyle \lim_{x \rightarrow c-} f(x)$.
(ii)
L is the right-limit of f(x) at c iff for any $\varepsilon > 0$, there exists $\delta > 0$ such that

 

\begin{displaymath}\mbox{if}\;\; c<x < c + \delta \;\;\ \mbox{then}\;\; \vert f(x) - L\vert < \varepsilon\end{displaymath}

 

and write $L = \displaystyle \lim_{x \rightarrow c+} f(x)$.

Of course, if a function has a limit when x get closer to c from both sides then the left and right limits exists and are equal to the limit at the point, i.e. if $\displaystyle \lim_{x \rightarrow c} f(x)$ exists then

 

\begin{displaymath}\lim_{x \rightarrow c+} f(x) = \lim_{x \rightarrow c-} f(x) = \lim_{x \rightarrow c} f(x)\;.\end{displaymath}

 

The following joke comes to my mind: An engineer, a physicist and a mathematician take a train ride through the Scottish countryside. Suddenly they see a sheep outside in a meadow. The engineer says: "Wow, in Scotland all sheep are black!" The physicist replies: "Not really; there is at least one black sheep in Scotland!" - The mathematician smiles and replies: "There is at least one sheep in Scotland with at least one black side." (My apologies to all engineers, who seem to be at the receiving end of most math jokes!).

What's the point? Whether you want to look at the limit world through the eyes of the "physicist" or the "mathematician" depends on your and your teacher's expectations! Maybe it suffices to stay with the "getting closer"-idea, maybe you need to dig into the workings of the formal $\varepsilon $-$\delta$ definition.

Example. Consider the function $\displaystyle f(x) = \frac{\vert x\vert}{x}$. We have

 

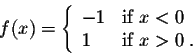
\begin{displaymath}f(x) = \left\{\begin{array}{lll} -1 &\mbox{if $x < 0$}\\ 1 &\mbox{if $x > 0$}\;.\\ \end{array} \right.\end{displaymath}

 

So obviously we have

 

\begin{displaymath}\lim_{x \rightarrow 0+} \frac{\vert x\vert}{x} = 1\;\;\mbox{and}\;\; \lim_{x \rightarrow 0-} \frac{\vert x\vert}{x} = -1\end{displaymath}

 

which implies that 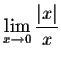$\displaystyle \lim_{x \rightarrow 0} \frac{\vert x\vert}{x}$ does not exist.

Example. Consider the function $f(x) = \displaystyle \sin\left(\frac{1}{x}\right)$. Let x get closer and closer to 0. For example we have

 

We see that f(x) does not get close to anything, even when x is close to 0 from the right, or the left. Thus $\displaystyle \lim_{x \rightarrow 0} \sin\left(\frac{1}{x}\right)$ does not exist. But this example is nastier than the previous one. In the previous example, the left and right limits did at least exist, but were not equal.

Example. Let f(x) = x2. It is easy to see that

 

\begin{displaymath}\lim_{x \rightarrow 2} x^2 = 4\;.\end{displaymath}

 

Let us show this through the formal definition. Indeed, let $\varepsilon > 0$. Since we want x to get close to 2, then we restrict ourselves to x between 1 and 3, i.e. $1 \leq x \leq 3$. Set $\delta = \frac{\varepsilon}{5}$. Then if $\vert x-2\vert < \delta$, then

 

\begin{displaymath}\vert x^2 - 4\vert = \vert(x-2)(x+2)\vert = \vert x-2\vert\;\vert x+2\vert \leq 5 \vert x-2\vert < 5 \delta = \varepsilon\;.\end{displaymath}

 

This finishes the proof of our claim.

Note that it was quite easy in this example to find $\delta$ but in general this can be quite a challenge. One may wonder how do we find the control number $\delta$? In general, we start our investigation from our conclusion: $\vert f(x) - L\vert < \varepsilon$, and try to come up with |x-c| through some algebraic manipulations. Let us illustrate this with an example:

Example. Consider the function $f(x) = \sqrt{x}$ and c = 9. Then we obviously have

 

\begin{displaymath}\lim_{x \rightarrow 9} \sqrt{x} = 3 \;.\end{displaymath}

 

Indeed, let $\varepsilon > 0$. We want to find $\delta > 0$ such that if $\vert x-9\vert < \delta $ then $\vert\sqrt{x} - 3\vert < \varepsilon$. But

 

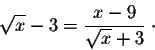
\begin{displaymath}\sqrt{x} - 3 = \frac{x-9}{\sqrt{x} + 3}\;\cdot\end{displaymath}

 

So if $\vert x-9\vert < \delta $, then

 

\begin{displaymath}\vert\sqrt{x} - 3\vert < \frac{\delta}{\sqrt{x} + 3} < \frac{\delta}{3}\;\cdot\end{displaymath}

 

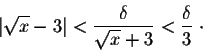
So if we choose 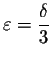$\varepsilon = \displaystyle \frac{\delta}{3}$, or equivalently $\delta = 3 \varepsilon$, then

 

\begin{displaymath}\vert x-9\vert < \delta \;\;\mbox{implies}\;\;\vert\sqrt{x} - 3\vert < \varepsilon\;.\end{displaymath}

 

In the following example, we discuss a limit at a "generic" point c.

Example. Let f(x) =x and g(x) = C, where C is a constant. Then for any point a, we have

 

\begin{displaymath}\lim_{x \rightarrow a} f(x) = \lim_{x \rightarrow a} x = a\end{displaymath}

 

and

 

\begin{displaymath}\lim_{x \rightarrow a} g(x) = \lim_{x \rightarrow a} C = C\;.\end{displaymath}

 

You may want to check these two statements by going through the $\varepsilon $-$\delta$ definition.

 

 

 

Exercise 1. Evaluate

 

\begin{displaymath}\lim_{x \rightarrow 1} \frac{x^2}{1 + x^2} \;\cdot\end{displaymath}

 

 

 

 

 

 

Exercise 2. Which of the statements below are true knowing that

 

\begin{displaymath}\vert x-2\vert < 0.1 \;\;\mbox{implies}\;\; \vert f(x) - 3\vert < 0.01?\end{displaymath}

 

(a)
$\displaystyle \lim_{x \rightarrow 2} f(x) = 3$;
(b)
$\displaystyle \lim_{x \rightarrow 3} f(x) = 2$;
(c)
If $\displaystyle \lim_{x \rightarrow 2} f(x) = L$, then 2.99 < L < 3.01.

 

 

 

 

 

 

 

 

Exercise 3. If $\displaystyle \lim_{x \rightarrow a} f(x) = L$ then

 

\begin{displaymath}\lim_{x \rightarrow a} \vert f(x)\vert = \vert L\vert\;.\end{displaymath}

 

What about the converse?

 

Back to the top of page

 

 

Send mail to m_engineer2002@netzero.com with questions or comments about this web site.
Copyright © 2001 Math Depot
Last modified: April 30, 2001