
By Rick Stoll
|
By Rick Stoll |
|
|
Integration is vital to many scientific areas. Many powerful mathematical tools are based on integration. Differential equations for instance are the direct consequence of the development of integration. So what is integration? Integration stems from two different problems. The more immediate problem is to find the inverse transform of the derivative. This concept is known as finding the antiderivative. The other problem deals with areas and how to find them. The bridge between these two different problems is the Fundamental Theorem of Calculus. What is the "area problem"? We want to find the area of a
given region in the plane. It is not hard to see that this problem can be
reduced to finding the area of the region
The answer to this problem came through a very nice idea. Indeed, let us
split the region
x0 = a < x1 < x2
< ... < xn = b
with xi + 1 - xi =  ,
for
i = 0, 1, ... , n - 1. ,
for
i = 0, 1, ... , n - 1.
Let
Area(
So we focus on the subregions The easiest way to choose a height for our rectangles is to choose the value of the function at the left (or right) end points of the small intervals [xi - 1, xi].
Let Li be the rectangle defined by the left-end point and Ri
be the rectangle defined by the right-end point. Then an approximation to
Area(
Area(L1) + Area(L2) + ...
+ Area(Ln) =
which we will call the left-sum denoted LEFT(n), and
Area(R1) + Area(R2) + ...
+ Area(Rn) =
which we will call the right-sum denoted RIGHT(n) Example. Consider the function
f (x) = x2
for x
x0 = 0 , x1 =
We have
LEFT(4) =
and
RIGHT(4) =
Note that Area( Indeed if the function f (x) is not too badly behaved, we will
show that when n gets larger, the numbers LEFT(n) and RIGHT(n)
get closer to
Area(
Area(
This is the main idea described above. The number Area(
Note that in the expression
Example. Let
This is true since the region Example. We have
Indeed, the region
The rectangle (depicted in red) is bounded above by x = a and
its area is a(b - a). The triangle (in blue) is determined
by the points: (a, a), (a, b), and (b, b).
Its area is
A precise definition for the definite integral involves partitions and lower as well as upper sums: Definition. A partition P of the interval [a, b] is a sequence of numbers {xi;i = 0, 1, ... , n} such that
x0 = a < x1 < x2
< ... < xn = b
For a function f (x) defined on [a, b] and a partition P of [a, b], set
mi = inf{f (x); x
for i = 1, ... , n, provided that f (x) is bounded on [a, b]. The sum
Lf(P) = m1(x1 - x0)
+ m2(x2 - x1) + ...
+ mn(xn - xn - 1)
is called the lower sum for f (x) over the partition P, and
Uf(P) = M1(x1 - x0)
+ M2(x2 - x1) + ...
+ Mn(xn - xn - 1)
is called the upper sum for f (x) over the partition P. Theorem. We have
Lf(P)
for any partition P of [a, b]. Moreover if f (x) is continuous on [a, b], except maybe at a finite number of points, and I is a number such that
Lf(P)
for any partition P of [a, b], then I = Area( This theorem is fundamental. Let us illustrate this with the following example. Example. Use the above theorem to show
where b
Uf(P) = x21(x1
- x0) + x22(x2
- x1) + ... + x2n(xn
- xn - 1)
and
Lf(P) = x20(x1
- x0) + x21(x2
- x1) + ... + x2n - 1(xn
- xn - 1) .
For each i, we have
xi - 12
since xi - 1
xi - 12(xi - xi - 1)
But
which implies
xi - 12(xi - xi - 1)
Hence
Lf(P)
since
(x13 - x03) + (x23
- x13) + ... + (xn3
- xn - 13) = b3 - a3
.
Exercise 1. Use similar ideas as used in the example above to show
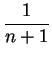 (bn
+ 1 - an + 1) (bn
+ 1 - an + 1)
where b
Exercise 3. Consider the function
|
|
Send mail to m_engineer2002@netzero.com with
questions or comments about this web site.
|