Home Up Search

Newtons Method
Calculus I
Calculus II
Chemistry
Physics
Oceanography

By Rick Stoll          

 Calc I

 

[Under Construction]

 

 

 

Already the Babylonians knew how to approximate square roots. Let's consider the example of how they found approximations to $\sqrt{2}$.

Let's start with a close approximation, say x1=3/2=1.5. If we square x1=3/2, we obtain 9/4, which is bigger than 2. Consequently $3/2>\sqrt{2}$. If we now consider 2/x1=4/3, its square 16/9 is of course smaller than 2, so $2/x_1<\sqrt{2}$.

We will do better if we take their average:

 

\begin{displaymath}x_2=\frac{1}{2}\left(x_1+\frac{2}{x_1}\right)=\frac{17}{12}.\end{displaymath}

 

If we square x2=17/12, we obtain 289/144, which is bigger than 2. Consequently $17/12>\sqrt{2}$. If we now consider 2/x2=24/17, its square 576/289 is of course smaller than 2, so $2/x_2<\sqrt{2}$.

Let's take their average again:

 

\begin{displaymath}x_3=\frac{1}{2}\left(x_2+\frac{2}{x_2}\right)=\frac{577}{408}.\end{displaymath}

 

x3 is a pretty good rational approximation to the square root of 2:

 

\begin{displaymath}x_3^2=332929/166464\approx 2.000006007305,\end{displaymath}

 

but if this is not good enough, we can just repeat the procedure again and again.

Newton and Raphson used ideas of the Calculus to generalize this ancient method to find the zeros of an arbitrary equation

 

\begin{displaymath}f(x) = 0 \;.\end{displaymath}

 

Their underlying idea is the approximation of the graph of the function f(x) by the tangent lines, which we discussed in detail in the previous pages.

Let r be a root (also called a "zero") of f(x), that is f(r) =0. Assume that $f'(r) \neq 0$. Let x1 be a number close to r (which may be obtained by looking at the graph of f(x)). The tangent line to the graph of f(x) at (x1,f(x1)) has x2 as its x-intercept.

 

 

From the above picture, we see that x2 is getting closer to r. Easy calculations give

 

\begin{displaymath}x_2 = x_1 - \frac{f(x_1)}{f'(x_1)} \;\cdot\end{displaymath}

 

Since we assumed $f'(r) \neq 0$, we will not have problems with the denominator being equal to 0. We continue this process and find x3 through the equation

 

\begin{displaymath}x_3 = x_2 - \frac{f(x_2)}{f'(x_2)} \;\cdot\end{displaymath}

 

This process will generate a sequence of numbers $\{x_n\}$ which approximates r.

This technique of successive approximations of real zeros is called Newton's method, or the Newton-Raphson Method.

Example. Let us find an approximation to $\sqrt{5}$ to ten decimal places.

Note that $\sqrt{5}$ is an irrational number. Therefore the sequence of decimals which defines $\sqrt{5}$ will not stop. Clearly $r = \sqrt{5}$ is the only zero of f(x) = x2 - 5 on the interval [1,3]. See the Picture.

 

 

Let $\{x_n\}$ be the successive approximations obtained through Newton's method. We have

 

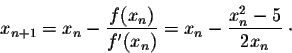
\begin{displaymath}x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} = x_n - \frac{x_n^2 - 5}{2x_n} \;\cdot\end{displaymath}

 

Let us start this process by taking x1 = 2.


 

\begin{displaymath}\begin{array}{cl} x_1=&2\\ x_2=&2.25\\ x_3=&2.2361111111111... ...7110\\ x_6=&2.236067977499789696409173668731276\\ \end{array}\end{displaymath}

 

It is quite remarkable that the results stabilize for more than ten decimal places after only 5 iterations!

Example. Let us approximate the only solution to the equation

 

\begin{displaymath}x = \cos(x) \;\cdot\end{displaymath}

 

In fact, looking at the graphs we can see that this equation has one solution.

 

 

This solution is also the only zero of the function $f(x) = x - \cos(x)$. So now we see how Newton's method may be used to approximate r. Since r is between 0 and $\displaystyle \frac{\pi}{2}$, we set x1 = 1. The rest of the sequence is generated through the formula

 

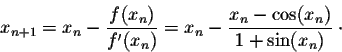
\begin{displaymath}x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} = x_n - \frac{x_n - \cos(x_n)}{1+ \sin(x_n)} \;\cdot\end{displaymath}

 

We have

 

\begin{displaymath}\begin{array}{cl} x_1=&1.\\ x_2=&0.7503638678402438930349423... ...7673873\\ x_8=&0.739085133215160641655312087673873 \end{array}\end{displaymath}

 

Exercise 1. Approximate the real root to two four decimal places of

 

\begin{displaymath}x^3 + 5x - 3 = 0\;.\end{displaymath}

 

 

 

 

Exercise 2. Approximate to four decimal places

 

\begin{displaymath}\sqrt[3]{3}.\end{displaymath}

 

 

 

 

 

Exercise 3. Show that Newton's Method applied to f(x)=x2-2 and x1=3/2 leads to exactly the same approximating sequence for the square root of 2 as the Babylonian Method.

 

 

 

Send mail to m_engineer2002@netzero.com with questions or comments about this web site.
Copyright © 2001 Math Depot
Last modified: April 30, 2001