Home Up Search

Vertical Tangants
Calculus I
Calculus II
Chemistry
Physics
Oceanography

By Rick Stoll          

 Calc I

 

[Under Construction]

 

 

 

In the definition of the slope, vertical lines were excluded. It is customary not to assign a slope to these lines. This is true as long as we assume that a slope is a number. But from a purely geometric point of view, a curve may have a vertical tangent. Think of a circle (with two vertical tangent lines). We still have an equation, namely x=c, but it is not of the form y = ax+b. In fact, such tangent lines have an infinite slope. To be precise we will say:

The graph of a function f(x) has a vertical tangent at the point (x0,f(x0)) if and only if

 

\begin{displaymath}f'(x) \rightarrow +\infty\;\;\mbox{or}\;\; f'(x) \rightarrow -\infty \;\;\mbox{as}\;\; x \rightarrow x_0\;.\end{displaymath}

 

Example. Consider the function

 

\begin{displaymath}f(x) = \sqrt[5]{2-x}\end{displaymath}

 

We have

 

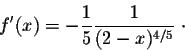
\begin{displaymath}f'(x) = -\frac{1}{5} \frac{1}{(2-x)^{4/5}}\;\cdot\end{displaymath}

 

Clearly, f'(2) does not exist. In fact we have

 

\begin{displaymath}\lim_{x \rightarrow 2} f'(x) = -\infty \cdot\end{displaymath}

 

So the graph of f(x) has a vertical tangent at (2,0). The equation of this line is x=2.

 

 

In this example, the limit of f'(x) when $x \rightarrow 2$ is the same whether we get closer to 2 from the left or from the right. In many examples, that is not the case.

Example. Consider the function

 

\begin{displaymath}f(x) = x^{2/3}\;.\end{displaymath}

 

We have

 

\begin{displaymath}f'(x) = \frac{2}{3} \frac{1}{x^{1/3}} \cdot\end{displaymath}

 

So we have

 

\begin{displaymath}\lim_{x \rightarrow 0+} f'(x) = +\infty \;\;\mbox{and}\;\; \lim_{x \rightarrow 0-} f'(x) = -\infty \cdot\end{displaymath}

 

 

 

It is clear that the graph of this function becomes almost vertical but then virtually doubles back on itself. Such pattern signals the presence of what is known as a vertical cusp. In general we say that the graph of f(x) has a vertical cusp at x0,f(x0)) iff

 

\begin{displaymath}f'(x) \rightarrow +\infty \;\;\mbox{as}\;\; x \rightarrow x_0... ... f'(x) \rightarrow -\infty \;\;\mbox{as}\;\; x \rightarrow x_0-\end{displaymath}

 

or

 

\begin{displaymath}f'(x) \rightarrow -\infty \;\;\mbox{as}\;\; x \rightarrow x_0... ...(x) \rightarrow +\infty \;\;\mbox{as}\;\; x \rightarrow x_0-\;.\end{displaymath}

 

In both cases, f'(x0) becomes infinite. A graph may also exhibit a behavior similar to a cusp without having infinite slopes:

Example. Consider the function

 

f(x) = |x3 - 8|.

 

Clearly we have

 

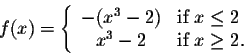
\begin{displaymath}f(x) = \left\{\begin{array}{cll} -(x^3 - 2) & \mbox{if $x \leq 2$}\\ x^3 - 2 & \mbox{if $x \geq 2$}. \end{array}\right.\end{displaymath}

 

Hence

 

\begin{displaymath}f'(x) = \left\{\begin{array}{rll} - 3x^2 & \mbox{if $x < 2$}\\ 3x^2 & \mbox{if $x > 2$}. \end{array}\right.\end{displaymath}

 

Direct calculations show that f'(2) does not exist. In fact, we have left and right derivatives with

 

\begin{displaymath}f'_-(2) = -12 \;\;\mbox{and}\;\; f'_+(2) = 12\;.\end{displaymath}

 

 

 

So there is no vertical tangent and no vertical cusp at x=2. In fact, the phenomenon this function shows at x=2 is usually called a corner.

Exercise 1. Does the function

 

\begin{displaymath}f(x) = \sqrt{9-x^2}\end{displaymath}

 

have a vertical tangent or a vertical cusp at x=3?

 

 

 

Exercise 2. Does the function

 

\begin{displaymath}f(x) = \left\{\begin{array}{rll} x^{1/3} + 3& \mbox{if $x \leq 0$}\\ 3-x^{1/5} & \mbox{if $x \geq 0$}. \end{array}\right.\end{displaymath}

 

have a vertical tangent or a vertical cusp at x=0?

 

 

 

Send mail to m_engineer2002@netzero.com with questions or comments about this web site.
Copyright © 2001 Math Depot
Last modified: April 30, 2001