Fiber Meets Fibonacci
Now...
 An old saying goes something like this, "Artists are born, not made."
For Billie Ruth Sudduth, this statement is not quite true. Billie Ruth, who
lives in the North Carolina mountains, makes baskets that are prized by
collectors from all across North America and have been displayed in the Renwick
Gallery of the Smithsonian Institution in Washington, D.C. She is
internationally known for her basket artistry and was the first woman to be
designated a Living Treasure by the state of North Carolina. But she was not
always a basket maker.
An old saying goes something like this, "Artists are born, not made."
For Billie Ruth Sudduth, this statement is not quite true. Billie Ruth, who
lives in the North Carolina mountains, makes baskets that are prized by
collectors from all across North America and have been displayed in the Renwick
Gallery of the Smithsonian Institution in Washington, D.C. She is
internationally known for her basket artistry and was the first woman to be
designated a Living Treasure by the state of North Carolina. But she was not
always a basket maker.
Billie Ruth experienced a typical childhood
while growing up in Birmingham, Alabama, and was interested in many hometown
activities, but creative arts was not one of them. "My mother and my
grandmother used to make hooked rugs, quilts, and do needlepoint. But I really
wasn’t interested in what they did." Instead of learning sewing crafts
from her mother and grandmother, she spent time playing sports with her
friends.
In school, Billie Ruth’s liberal arts studies
included only the basic mathematics needed to get into college: algebra 1,
geometry, and algebra 2. "I really didn’t care for math. It didn’t
seem important to me at the time. I didn’t do well in my math classes, even
though I always got top scores in any national tests in math." Her lack of
enthusiasm for mathematics was to change sometime later, however.
Billie Ruth attended Huntington College in Alabama as an undergraduate,
focusing on psychology and social issues. She continued her concentration in
psychology and social work while pursuing a graduate degree at the University
of Alabama, subsequently working as a school psychologist for nearly twenty
years. So how did she work baskets into her schedule?
About fifteen years ago, after a particularly tiring school year, summer found
Billie Ruth exhausted, both mentally and emotionally. A colleague suggested
that she take a basket-weaving course. "I was already a collector of
baskets, so I figured that maybe I could make one of my own. At the same time,
I could get my mind off school for a bit and maybe learn something that could
serve as a relaxation activity for other times when I became stressed."
That one basket-weaving class was a turning point in Billie Ruth’s life.
"I knew within the first fifteen minutes of the class that this was what I
wanted to do for the rest of my life. I loved working with the basket materials
and producing baskets. Something about the materials and the process resonated
with me. Working with the natural materials captured my attention. I soon
developed a real passion for crafting these baskets." In time, Billie Ruth
began working a full day at school and then spending most of the evening making
baskets. At first she adopted the time-honored techniques of basket making, but
eventually she developed her own style. "I really wasn’t sure what the
style was. I made baskets that just seemed to flow. The ones I liked best were
also the ones people responded to." Among Billie Ruth’s collectors were
professionals, such as stock brokers, architects, and engineers, whose work
involved mathematics. Billie Ruth started to bring her basket-making talent
into school by teaching her craft. A teacher in one school pointed out to
Billie Ruth that her baskets and their designs incorporated the golden ratio,
as shown by the ratios between height and width of her baskets and the spacing
between patterns on the baskets. "Suddenly, everything I had been doing
fell into place. The baskets that most clearly reflected the golden ratios were
the ones I felt were my best, and those were the ones that seemed to sell
fastest. What I had been doing intuitively I now could understand. I could now have a purpose behind my basket
making."
<go to top>
Billie Ruth had been weaving the golden ratio into her baskets on instinct.
Her conscious use of this element has resulted in even more spectacular pieces.
"Now that I know how to use the golden ratio in my baskets, I have made
even more applications of it. I have developed more complex patterns using the
golden ratio. It is really exciting for me to see how these designs look on a
finished basket," she explains.
Billie Ruth now designs baskets so that the ratio of the width to the height
approximates the golden ratio. She also uses what she calls "nature’s
sequence" for the weaving pattern. A typical basket weave alternates
between over and under weaves. A nature’s-sequence weave is one over, one
under, two over, and three under. These numbers are the first four terms of the
Fibonacci sequence, in which each new term (after the first two terms) is the
sum of the preceding two terms. The ratio of each term to its predecessor gets
closer and closer to the golden ratio as you extend further into the sequence.
Billie Ruth also uses the golden ratio in line designs of her baskets. The
zig-zag design is not random. "I call one pattern the ‘Fibonacci Five’
because it follows the Fibonacci sequence in the way the lines zig and zag on
the basket." For example, beginning at the bottom, a line in ‘Fibonacci
Five’ will zig at five rows from the bottom.

The next zig comes eight rows later then continues to zig and zag at intervals of
thirteen, twenty one, and thirty-four rows." What had been an instinctive
design for her baskets has now become a highly mathematical design that meets
specific mathematical relationships in the size of the basket, its weave, and
its line designs.
Billie Ruth thinks that somewhere back in high school she had heard of the
golden ratio and Fibonacci, but she is not sure. "If had known about the
golden ratio and the Fibonacci sequence when I started making baskets, it would
have helped me a lot. I could have found the techniques I use now a lot
earlier, and wouldn’t have had to struggle to find the basket designs I like
to make." Billie Ruth took very few mathematics courses after high school.
"I wish I had taken more mathematics in high school and college. At the
time, I thought, ‘What do I need this for?’ I couldn’t see why it would
do me any good. It was only when I needed a graduate math course that I took
one. By then I could see the relevance of it to what I wanted to do, and I did
fine.
<go to top>
"I am sure students today feel like I did about math and think they
will never use it. Well, look at me. I make baskets for a living, and I use
math all the time. I wish I had taken more math. Now I am experimenting with
making spiral designs on my baskets and I need to know more about logarithms
and fractals. So I have to teach myself these things now because I didn’t
take the right courses in high school and college."
Billie Ruth’s baskets are made with two main colors. She uses black or red
on her walnut-colored materials. "I think black stands out the best to
show a pattern, and I use red because no one else knows how to make the
permanent red dye that I do." All of Billie Ruth’s dyes are natural,
something she adopted when she first started making baskets. "The American
Indians, like the Cherokee and Choctaw, used only natural dyes. They had a
respect for the earth, and I think that by using natural materials and the
golden ratio, I show the same respect for the earth that they have shown for so
many centuries."
One of Billie Ruth’s baskets is in the American Embassy in Niger because
her work blends well with the African baskets created by native basket makers.
"I think it has to do with the Fibonacci ratios," says Billie Ruth.
"The golden ratio is found in so many places in nature that it only makes
sense that different cultures would incorporate it into their designs and that
different peoples would respond to artwork that reflects the golden
ratio."
Billie Ruth is not just a basket maker. She spreads the word about art and
mathematics by visiting schools and working with students and teachers.
"When I left my school position and started to make baskets full time, I
missed the kids. Being an artist is an individual, almost private pursuit, and
I needed to connect with kids. By visiting schools, I can do that and still be
a basket maker."
<go to top>
... & Then
The Shape of Things to Come
The history of the golden ratio stretches back
thousands of years to ancient Egypt. The pyramids, statues of Egyptian gods and
pharaohs, and even Egyptian hieroglyphics show the golden ratio in their
proportions. A royal decree to artisans and architects alike was that they
include suq, the golden ratio, in some facet of their work.
 The golden ratio next appeared in the Brotherhood of Pythagoreans. This mystical,
religious group was headed by Pythagoras (c. 570 b.c.—500 b.c.), who is best
remembered for the Pythagorean theorem, relating the lengths of three sides of
a right triangle(a2 + b2 = c2). As a group, the Brotherhood of Pythagoreans viewed numbers as
being sacred in their cosmology and adopted the five-pointed star, or
pentagram, as its emblem (see fig. 2). The pentagram is replete with the golden
ratio in many comparisons of its segment lengths. Every pentagram has a regular
pentagon at its center. Drawing in the diagonals of this pentagon results in
another pentagram with a new set of segments whose lengths can be compared to
obtain the golden ratio. Inside this pentagram is another pentagon inside of
which can be constructed still another pentagram. This process can be continued
indefinitely, resulting in an infinite number of examples of the golden ratio.
The golden ratio next appeared in the Brotherhood of Pythagoreans. This mystical,
religious group was headed by Pythagoras (c. 570 b.c.—500 b.c.), who is best
remembered for the Pythagorean theorem, relating the lengths of three sides of
a right triangle(a2 + b2 = c2). As a group, the Brotherhood of Pythagoreans viewed numbers as
being sacred in their cosmology and adopted the five-pointed star, or
pentagram, as its emblem (see fig. 2). The pentagram is replete with the golden
ratio in many comparisons of its segment lengths. Every pentagram has a regular
pentagon at its center. Drawing in the diagonals of this pentagon results in
another pentagram with a new set of segments whose lengths can be compared to
obtain the golden ratio. Inside this pentagram is another pentagon inside of
which can be constructed still another pentagram. This process can be continued
indefinitely, resulting in an infinite number of examples of the golden ratio.
Several decades after Pythagoras died, the Brotherhood of Pythagoreans faded
into obscurity, but the golden ratio did not. It continued to be an important
element in life, especially in classical Greek architecture and notably in the
Parthenon in Athens. Inside the Parthenon was a forty-foot-tall statue of the
goddess Athena that also showed the golden ratio in its proportions. Both the
temple and the statue were designed by Phidias (c. 485 b.c.—430 b.c.), the
first artist known to use the golden ratio extensively in his work. It is
fitting that the symbol for the golden ratio is the Greek letter phi, f, the
first letter in Phidias’s name.
<go to top>
Over a century later, Euclid (c. 300 b.c.) discussed what is currently known as
the golden ratio in his classic work The Elements. Segment AC shown here:

is divided by point B in such a way that the following relationship is true:

Euclid did not use algebraic representations of the golden ratio, but
succeeding mathematicians did. In the preceding diagram, if AB = 1 and BC = x,
then the proportion becomes:
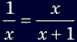
When this proportion is solved for x,
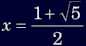
<go to top>
Thus,

or about 1.6.
Following Phidias, many artists and artisans used the golden ratio in some
form or another in their work, whether in proportions of the human face and
body or in architecture. In 1509, Leonardo da Vinci (1452—1519) illustrated
for Italian mathematician Luca Pacioli (1445—1514) a mathematics text titled
De divina proportionale (The Divine Proportion). In his book, Pacioli showed
the golden ratio in many different settings, from the human form to buildings
and paintings; however, da Vinci first used the term "golden
section," or golden ratio.
One name that is inextricably linked to the golden ratio is Leonard of Pisa
(1180—1250), better known as Fibonacci. He was one of the most accomplished
mathematicians in Europe since the time of the ancient Greeks. He learned the
mathematics of the time while accompanying his merchant father on visits to the
Islamic seaports of the Mediterranean and North Africa. During these business
travels, Fibonacci probably encountered what was then a new way of writing
numbers–the Hindu-Arabic positional system of ten digits that we use today.
Fibonacci was one of the first European mathematicians to use the new system,
and in his work Liber Abaci (1202), he strongly advocated its use. Liber Abaci
was a seminal work for several reasons. First, it was one of the first
western-European books to use and advocate Hindu-Arabic numbering. Second, it
was the outstanding mathematics book of the century. Third, it contained the
rabbit problem, already discussed in the student activity. As terms are added
to the sequence of numbers representing each of the rabbit pairs in each month,
the ratio of each new term to its preceding term approaches the golden ratio.
<go to top>
It was left to a Scottish mathematician some
centuries later to make the connection between the golden ratio and
Fibonacci’s rabbit problem. Robert Simson (1687—1768), a geometer known for
his translation of Euclid’s Elements, noticed that consecutive terms of the
solution to the rabbit problem (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, . . . )
showed the golden ratio; for example,
55/34 »
1,618
 Some years earlier, Johannes Kepler (1571—1630), famous for his model of the solar
system, had coined the term "divine section." He said, "Geometry
has two great treasures: one is the theorem of Pythagoras; the other, the
division of a line into extreme and mean ratio [golden ratio]. The first we may
compare to a measure of gold; the second we may name a precious jewel."
Kepler first noticed that leaf arrangements on some plants and petals on some
flowers follow the pattern of what is now called the Fibonacci sequence.
Some years earlier, Johannes Kepler (1571—1630), famous for his model of the solar
system, had coined the term "divine section." He said, "Geometry
has two great treasures: one is the theorem of Pythagoras; the other, the
division of a line into extreme and mean ratio [golden ratio]. The first we may
compare to a measure of gold; the second we may name a precious jewel."
Kepler first noticed that leaf arrangements on some plants and petals on some
flowers follow the pattern of what is now called the Fibonacci sequence.
Since Kepler’s time, the golden ratio has been found in many natural
settings, including snail shells, ram horns, pinecones, and even the DNA
spiral. Today, the Fibonacci Society, a group interested in the golden ratio,
continues to discover and apply the Fibonacci sequence in a wide range of human
and natural representations.
<go to top>
 An old saying goes something like this, "Artists are born, not made."
For Billie Ruth Sudduth, this statement is not quite true. Billie Ruth, who
lives in the North Carolina mountains, makes baskets that are prized by
collectors from all across North America and have been displayed in the Renwick
Gallery of the Smithsonian Institution in Washington, D.C. She is
internationally known for her basket artistry and was the first woman to be
designated a Living Treasure by the state of North Carolina. But she was not
always a basket maker.
An old saying goes something like this, "Artists are born, not made."
For Billie Ruth Sudduth, this statement is not quite true. Billie Ruth, who
lives in the North Carolina mountains, makes baskets that are prized by
collectors from all across North America and have been displayed in the Renwick
Gallery of the Smithsonian Institution in Washington, D.C. She is
internationally known for her basket artistry and was the first woman to be
designated a Living Treasure by the state of North Carolina. But she was not
always a basket maker.
 The golden ratio next appeared in the Brotherhood of Pythagoreans. This mystical,
religious group was headed by Pythagoras (c. 570 b.c.—500 b.c.), who is best
remembered for the Pythagorean theorem, relating the lengths of three sides of
a right triangle(a2 + b2 = c2). As a group, the Brotherhood of Pythagoreans viewed numbers as
being sacred in their cosmology and adopted the five-pointed star, or
pentagram, as its emblem (see fig. 2). The pentagram is replete with the golden
ratio in many comparisons of its segment lengths. Every pentagram has a regular
pentagon at its center. Drawing in the diagonals of this pentagon results in
another pentagram with a new set of segments whose lengths can be compared to
obtain the golden ratio. Inside this pentagram is another pentagon inside of
which can be constructed still another pentagram. This process can be continued
indefinitely, resulting in an infinite number of examples of the golden ratio.
The golden ratio next appeared in the Brotherhood of Pythagoreans. This mystical,
religious group was headed by Pythagoras (c. 570 b.c.—500 b.c.), who is best
remembered for the Pythagorean theorem, relating the lengths of three sides of
a right triangle(a2 + b2 = c2). As a group, the Brotherhood of Pythagoreans viewed numbers as
being sacred in their cosmology and adopted the five-pointed star, or
pentagram, as its emblem (see fig. 2). The pentagram is replete with the golden
ratio in many comparisons of its segment lengths. Every pentagram has a regular
pentagon at its center. Drawing in the diagonals of this pentagon results in
another pentagram with a new set of segments whose lengths can be compared to
obtain the golden ratio. Inside this pentagram is another pentagon inside of
which can be constructed still another pentagram. This process can be continued
indefinitely, resulting in an infinite number of examples of the golden ratio.
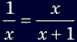
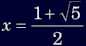

 Some years earlier, Johannes Kepler (1571—1630), famous for his model of the solar
system, had coined the term "divine section." He said, "Geometry
has two great treasures: one is the theorem of Pythagoras; the other, the
division of a line into extreme and mean ratio [golden ratio]. The first we may
compare to a measure of gold; the second we may name a precious jewel."
Kepler first noticed that leaf arrangements on some plants and petals on some
flowers follow the pattern of what is now called the Fibonacci sequence.
Some years earlier, Johannes Kepler (1571—1630), famous for his model of the solar
system, had coined the term "divine section." He said, "Geometry
has two great treasures: one is the theorem of Pythagoras; the other, the
division of a line into extreme and mean ratio [golden ratio]. The first we may
compare to a measure of gold; the second we may name a precious jewel."
Kepler first noticed that leaf arrangements on some plants and petals on some
flowers follow the pattern of what is now called the Fibonacci sequence.