| home | stands | games | about | mpjournal | back | links |
The ancient Egyptians were using special symbols, known as pictographs, to write down numbers over 3,000 years ago. Later, the Romans developed a system of numerals that used letters from their alphabet rather than special symbols. Today, we use numbers based on the Hindu-Arabic system. We can write down any number using combinations of up to 10 different symbols (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9). The ancient Egyptians developed number systems to keep accounts of what was bought and sold.
We use numbers every day and tend to take them for granted. But how did the
idea of numbers arise? Did every culture develop the ideas of counting and
numbers separately or have these ideas arisen in only a few cultures and then
spread, for example, through trade? Is counting intuitive or did it arise to
solve particular problems?
Some of the oldest evidence of counting so far discovered comes from ancient artifacts
belonging to groups of hunters and gatherers. For example, a wolf
bone, dated about 30,000 BC, has been discovered with a series of notches carved
in it, which seem to represent a tally of some kind.
Tallying seems likely to be among the earliest methods of keeping a record of
quantities and appears in many cultures. But is this really counting? For
example, a tally system might be used to keep track of a flock of sheep. A small
stone might be put in a pile for each sheep as it is let out to graze in the
morning and then a stone could be removed from the pile again for each sheep as
it was collected in at night. Any pebbles left over would indicate that some
sheep were missing. This is really only a straight comparison between two sets
of objects, the stones and the sheep. It does not give any idea of the actual
number of sheep in the flock.
Another idea sometimes found at an early developmental stage of a culture is
that of different number words being used depending on the context. For example,
there might be one word for four people and another for four stones. At some
stage an abstract idea of number develops and the concept of, for example,
"threeness", where a group of three fish and three stones are
perceived to have something in common, is incorporated into the system.
Do humans have an intuitive knowledge of numbers, or do cultures develop numbers
and counting to solve particular problems? There is no single answer to this
question and it is the subject of much debate. However, there are cultures that
have number systems consisting only of words for one, two, and many. For
example, certain Australian aboriginal tribes use this system, but, if children
from these tribes are taught to use other number systems, there is no
significant difference between their mathematical abilities and those of
children of other cultures. Perhaps this fact provides some evidence for numbers
and counting having arisen in response to particular needs. The words for three
in some European languages are very similar to the words for beyond or over. For
example, the word for three in Latin is tres, which is similar to the word
meaning beyond, trans. Perhaps these systems were also one, two, many systems
originally, with words for different types of "many" only being
developed later.
The one, two, many system has been extended by some cultures to form the
2-system. This allows the representation of groups of three or four objects by
repeating the words for one or two. Thus, three would be two-one, and four would
be two-two. We might wonder why, having got this far, counting was not continued
indefinitely. However, again, this is not really counting. The words are being
used to describe particular states, and do not include the idea of an increasing
series of numbers.
The development of ordinal numbers (first, second, third, etc.) from cardinal numbers (one, two, three, etc.) may have happened as a result of finger counting. Fingers, and sometimes toes, can be used to count on. If this is always done in the same order, then the same finger will always be used to represent, for example, seven. This provides a link between the seven items being counted and the seventh finger in the sequence. This link is not provided if we use stones as a tally. Any pebble in a pile could be the seventh one; they are not counted in any particular order.
Counting is nearly as old as speech and numerals are as old as writing. In ancient times, and in some instances down to modern times, each language had its series of numerals. Thus the number of systems of notation employed was about the same as the number of written languages, and in some cases a single language had several systems.
In pictographic notation the number is given by repetitions of the symbol
representing the object in question. For example, "five men" would be
represented by the symbol for "man" repeated five times.
Many cultures throughout history have represented numbers by repetitions of a
vertical or horizontal stroke, 1 by one stroke, 2 by two strokes, etc. In
various forms of speech the number five is expressed by the word
"hand" or "the hand finished", and ten by "two
hands" or "two hands finished". In some South American languages
"all the fingers" means ten; "all the fingers and toes", 20;
"fingers and toes of two men", 40; "one of the other hand",
six; "foot one", 11; "foot two", 12; and so on.
Hieroglyphic number systems consisted of repetitions of a single unit, with the use of hieroglyphics (pictures or symbols) for higher numbers. These systems sometimes introduced the principle of multiplication when repetitions became too many for practical use.
The Egyptians had three systems of writing, the hieroglyphic, the hieratic, and
the demotic writings. The hieroglyphic system was the sacred writing reserved
for formal inscriptions and was usually used for writing on stone. Numbers were
seldom used in this system. Hieroglyphics were too complex for everyday use and
this led to the development of a simpler system, hieratic or temple writing.
This was used by priests and scribes for everyday records and was mostly used
for writing on papyrus. Demotic writing developed from hieratic writing and was
the system of writing used in everyday life.
Egyptian numbers were written from right to left. They started at one and went
up to a million. The numbers one to nine were written as combinations of
vertical strokes, ten was represented by a sign that looks like an upturned U,
100 by a coil of rope, 1000 by a sign representing a lotus flower, 10,000 by a
vertical finger, 100,000 by a tadpole, and 1 million by a man with upraised arms
(see Diagram 1).
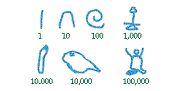
The Sumerians are thought to have invented writing in the 4th-2nd millennia BC.
They used symbols incised in clay with a stylus to record words and numbers. The
Sumerian number system was a base 60 or sexagesimal system. We can still see
traces of a base 60 system in the current use of hours, minutes, and seconds to
measure time and degrees (360 in a circle) to measure angles.
The Sumerians had only two numerals, one and ten. They also had a place-value
system. The columns, reading from the right, increased by a factor of 60. Thus
the Arabic (base ten) number 46,940 can be represented as in Diagram 2.

One drawback of the Sumerian system was the lack of a way to represent zero. For example, it would be impossible to tell if the number shown in Diagram 3 represented 421, 4210, 4021, or any other variation, although it might have been possible to tell which meaning was intended from the context.
The Babylonians also used clay for writing. They incised numbers with a stylus
that left wedge-shaped marks. This resulted in the writing system being known as
cuneiform, from cuneus, meaning a wedge, and forma, meaning a shape. The
Babylonian system used a mixture of base ten and base sixty. Base sixty tended
to be used for larger numbers.
The numerical notation for small numbers was quite simple; one was represented
by a short, straight, vertical stroke, or wedge, two to nine by two to nine
short strokes, 10 by an angle, and 100 by a short vertical wedge followed by a
short horizontal wedge (see Diagram 4).

Sometimes 10 was represented by a vertical crossed by a horizontal stroke, 20 by a vertical crossed by two horizontals, etc., and the units were represented by horizontal rather than vertical strokes. The tens were sometimes represented by circles, and the units by a kind of crescent. In larger numbers, which were not standardized, the vertical stroke also stood for 60, 3600, and in general for 60n, where n is a positive integer. The angle also stood for 10 × 60, 10 × 3600, etc., and in general for 10 × 60n. The value to be taken depended entirely upon the context. The Babylonians also had a place-value system so it was usually clear what each symbol was being used to represent in a number. For example, 11 would be represented by the symbol for ten followed by the symbol for one (or sixty), whereas 70 would be the represented by the same two symbols in reverse order. Sometimes the symbols for one and sixty were different sizes.
The Babylonians also developed a way of representing zero, an important advance in the history of numbers since it eliminated any possible confusion over whether a number such as 316 was intended to represent 316, 3160, 3016, 3106, etc. Initially, Babylonian scribes represented zero by leaving a large gap between numerals, but, later, a special symbol was invented. For example, the Arabic number 3608 could be represented by the symbol for 3600 followed by the symbols for 0 and 8, as in Diagram 5.
Another development of the Babylonian number system was the occasional use of a minus sign to represent a number that was just less than an exact number of tens. For example 29 could be represented as in Diagram 6.
The Chinese had, and still have, various numerical systems. The rod or stick numerals, derived from the wooden sticks used on counting boards, are quite simple. These numerals were frequently written in the monogram form, as in Diagram 7.

The diagram shows the numbers 0 to 90 and the number 46,431 written in monogram
form.
Apart from the rod system, the Chinese have several other systems of numerals,
including the "common" numerals (hsiao-hsieh), and the
"official" numerals, which are highly decorated versions of the common
numerals used on documents to prevent fraud. Since 1955 it has been government
policy to introduce Arabic numerals.
The different Chinese systems have a variety of symbols for zero. The symbol for
zero in the rod system can be seen in the above diagram.
The Mayan and Aztec number systems were vigesimal (base twenty) systems rather
than denary (base ten) systems such as those in widespread use today.
In the Mayan system, the numbers 1 to 4 were represented by dots and 5, 10, and
15 by sticks, lines, or bars. The moon may have been used to represent 20. The
symbols used for the multiples of 20 (400, 8000, 160,000, etc.) are still
uncertain. It is now thought unlikely that the Mayans used a place-value
notation.
In the Aztec system, the numbers 1 to 19 were represented by dots or circles, 20
by a religious banner, 400 (20 × 20) by a pine tree, and 8000 (20 × 20 × 20)
by an incense-pouch.
The Mayan system also used a symbol to represent zero; this symbol was similar
to a shell, having numerous variants. The highest number found in a Mayan
inscription is 1,814,639,800 days, corresponding to over 5,100,000 years.
A number of civilizations have used the letters of their alphabets for numerical symbols, taking the first letter for 1, the second for 2, the tenth for 10, the eleventh for 20, and so forth.
One of these systems is the Hebrew number system. The 22 letters of the Jewish alphabet were used to represent the numbers up to 400. In the Talmud the numbers above 400 are formed by composition, for example, 500 = 400 + 100 and 900 = 400 + 400 + 100; in later times the final forms of the letters k, m, n, p, and ts were used for 500, 600, 700, 800, and 900, respectively. The later Hebrew number system is shown in Diagram 1.

The thousands were represented by the same letters as the units, sometimes followed by a kind of apostrophe.
The Greeks had two number systems, the earliest of which was used from the 5th to the 1st centuries BC. These numbers were known either as Herodian numbers (after the writer from the 2nd century who described them) or as Attic numbers (after the Attic inscriptions in which they occur). This system uses the initial letters of the number words to represent the numbers. Thus, G (an old form of P, initial of PENTE, pente), was used to represent 5; D (DEKA, deka), 10; H (HEKATON, hekaton), 100; X (XILIO, khilioi), 1000; and M (MYPIOI, murioi), 10,000. These numerals were often combined with the symbol for 5 to create numerals for numbers such as 15, 50, 500, and 5000. The Herodian numbers are shown in Diagram 2.

Tens of thousands were sometimes indicated by dots. Sometimes special symbols
were used for fractions, and an accent or a line above the numeral might
indicate the fraction.
The later Greek number system used the letters of the Greek alphabet for
numerical notation in the same way as the Hebrew system did. Since they had only
24 letters in their classical alphabet, and for a more satisfactory system of
numerals they needed 27 letters, they retained the ancient letters digamma (as
6), koppa (as 90), and sampi (as 900). To distinguish the numerals from letters
a bar was commonly written over each number, but sometimes the letter was
written as if lying on its side. Thousands were often indicated by placing a bar
to the left of the number. In modern Greek type, the thousands are indicated as
in Diagram 3.

Diagram 3: The Later Greek Number System
Roman numerals are among the most enduring of number systems. Indeed, they are
still in use today for certain purposes, such as numbering appendices in books,
denoting dates in the credits of films and television programmes, and on watches
and clocks. The long usage of Roman numerals could be due to a number of
factors, including the widespread influence of the Roman Empire, the force of
tradition, and the fact that the system had many advantages over other European
systems of the time. For example, Roman numbers had the advantage that the
majority of users had to memorize only a few symbols and their values.
The origin of the Roman number system is still obscure. One theory is that it
may have been based on the number 5. Thus, the symbol for 5, V, could have its
origins in a representation of a hand held flat with the fingers together, and
X, for 10, could be a double V. Three of the other symbols could have come from
Greek letters not needed in the early Roman alphabet: C (100) from theta (q), M
(1000) from phi (f), and L (50) from chi (c, also written as
^). q and f were
probably changed gradually, under the influence of the initials of the number
words centum (100), and mille (1000), to C and M.
The modern system of Roman numerals uses a subtractive principle. For example, 4
is written as IV, five minus one, rather than IIII, 9 is written as IX, ten
minus one, rather than VIIII, and 900 is written as CM, 1000 minus 100, rather
than DCCCC. Thus, for example, 1996 is written as MCMXCVI. The modern set of
Roman numerals can be seen in Diagram 4.

Diagram 4: Modern Roman Numerals
It is clear that the Romans used some very large numbers. For example, an inscription on the columna rostrata, commemorating the Roman victory off Mylae (Milazzo) in the First Punic war (260 BC), has a symbol for 100,000 repeated 23 times (= 2,300,000).
Pi, which is represented by the Greek letter p, is one of the oldest mathematical quantities known to humanity. It denotes the ratio of the circumference of a circle to its diameter. In other words, it is the number of times the diameter of a circle will fit around the edge of the circle. This is the same for all circles and is approximately 3.14. p is the first letter of the Greek word perifereia, meaning circumference.
p is an irrational number; it cannot be expressed as a ratio of two integers,
and its expression as a decimal never terminates and never starts recurring. In
fact the numbers in the decimal expression of p seem to be almost
"random" - there is no perceivable pattern in their order.
Not only is p irrational, it is also a transcendental number. This means that it
is not the solution of any polynomial equation with coefficients that are
rational numbers.
The origins of p are so ancient that they are now untraceable. It is possible
that p first became known in Egypt. There is a reference to
p in the Egyptian
Rhind Papyrus, dated about 1650 BC. The first theoretical calculation is likely
to have been carried out by Archimedes around 200 BC. He found that the value of
p is between 223/71 and 22/7.
No further advances were made until the 17th century. p
was then known as the
Ludolphian number, after Ludolph van Ceulen, a German mathematician. In the 17th
century the search for mathematical formulas for p began. One of the most well
known of these is the infinite series:
![]()
This series is sometimes attributed to Gottfried Leibniz but it seems to have
been first proposed by James Gregory (1638-1675). It does not actually help us
to calculate p at all. To find the first four decimal places of
p correctly, we
would need to find the first 10,000 terms of the series.
However, the search for mathematical formulas for p continued. In 1706, the
English mathematician John Machin found a formula that enabled the calculation
of p to any number of decimal places. The calculation was still time-consuming
and repetitive, with a single mistake disrupting all further stages of the
process. In 1873, Shanks calculated p to 707 decimal places. Unfortunately he
made a mistake when calculating the 528th decimal place so that he only got the
first 527 correct.
p was proved to be irrational by the Swiss-German mathematician Johann Lambert
in 1761. In 1882, the German mathematician Carl Louis Ferdinand von Lindemann
proved that p is a transcendental number. The symbol
p was first used with its
present meaning by the Welsh mathematician William Jones in 1706. Leonhard Euler
adopted the notation in 1737 and it quickly became standard.
With the advent of computers, it became possible to find p
to many more decimal
places. In June 1995, the Japanese mathematician Yasumasa Kanada found p
correct
to 3,221,220,000 decimal places. In theory, p can be calculated to any desired
degree of accuracy because its decimal expansion goes on for ever. In practice, p
calculated to 39 decimal places would be enough to allow us to find the
circumference of a circle around a sphere with a radius of 15 billion light
years (the distance to some of the most remote objects in the universe) to
within an accuracy of the radius of a hydrogen atom.
Many mnemonics have been invented to help remember the decimal representation of
p. The following one gives the first 15 digits: "How I want a drink,
alcoholic of course, after the heavy lectures involving quantum mechanics."
Each word is replaced by the number of letters in it. Thus, p
= 3.14159265358979….
The Arabic numerals, 0, 1, …, 9, now in general use, are derived from Indian numerals. The name Arabic is used because Western Europeans learned about the system from Arabic writers.
The history of Indian-Arabic numerals is only vaguely known because few examples of their early use have survived. Early forms of the numerals were developed in India between the 2nd century BC and the 6th century AD. During that period Indian mathematicians realized that a place-value system of notation (see below), which included a symbol for zero, enabled calculations to be performed by simply writing down numbers instead of using an abacus. The numerals themselves were used in several sites around the Mediterranean but only as simple ways of writing down numbers. Methods of calculation that used the numbers were not understood outside India until the Arabic mathematician Al-Khwarizmi wrote a treatise on them in the early 9th century. Al-Khwarizmi's treatise was not translated into Latin until the early 12th century and the method of calculation by writing down numbers became known as "algorism" (a corruption of al-Khwarizmi). In the late 12th century, Leonardo Fibonacci started to publish books in Pisa that showed the full power of the Arabic number system and it was taken up by the book-keepers and commercial men of northern Italy. For several centuries there was great controversy over whether algorism or the abacus was the fastest method of calculating. With the invention of printing, numerous books describing algorism appeared and, from about 1500 onwards, the Arabic number system became standard in Western Europe. The cumbersome Roman numerals were inadequate for writing out the large and complicated numbers used in astronomy and, increasingly, in other branches of science, and the invention in the early 17th century of logarithms finally ended their use.
The most important feature of the Arabic number system is the use of place-value notation. Perhaps the best way to see how this works is to imagine that counting is carried out by threading beads onto wires arranged as in Diagram 1.
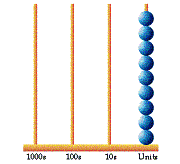
Diagram 1: A Representation of the Place-value Notation
As each object is counted it is represented by a single bead threaded on the right-hand end wire. The wire has only enough room for nine beads. To count the tenth object, one bead is put on the next wire and all beads are taken off the end wire. Then the beads are used to fill up the end wire again, and so on. Thus each bead on the second wire represents ten; on the third wire one hundred; on the fourth wire one thousand, and so on. To write this down, all that are needed are nine symbols to represent from one to nine beads (in this case, the Arabic numerals 1 to 9) and one symbol (in this case, 0) to represent an empty wire. The symbols are written out in the same places as the wires: the value of a numeral depends on its place. For example, in Diagram 2, we can see that 4305 is a way of representing the number that consists of 4 thousands, 3 hundreds, 0 tens and 5 units or ones.
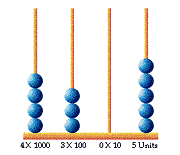
Diagram 2
Ten is called the base, or radix, of this system, which is the one now in
everyday use. A notation system with ten as the base is called a denary system.
Any other number could be used as a base.
Place-value notation is very difficult without a symbol for zero. If there were
no zero symbol in the denary system then 9 could mean nine, ninety, nine
hundred, etc. Zero may be a late invention in the history of numbers, although
Hindu literature suggests it was in use before the time of Christ.