| home | stands | games | about | mpjournal | back | links |
Number Theory
Goldbach's Conjecture
Fermat's Last TheoremIntegersGaussian IntegersPrime NumbersThe Sieve of Eratosthenes
The Fundamental Theorem of Arithmetic
How Many Primes Are There?An Infinity Of Primes
Mersenne Numbers
Largest Prime Numbers
Famous TheoremsDiophantine EquationsSolving Diophantine EquationsFermat's Last TheoremHistory of the Theorem
Proof Of The TheoremNumber theory is the branch of mathematics concerned with studying the properties and relations of integers. Many of these problems are concerned with the properties of prime numbers. Number theory also includes the study of irrational numbers, transcendental numbers, Diophantine equations, and continued fractions. There are a number of branches of number theory, including algebraic number theory, analytic number theory, geometric number theory, and probabilistic number theory. Algebraic number theory is the study of numbers that are the roots of polynomial equations with integer coefficients, and includes the study of Gaussian integers.
One of the most famous problems in number theory is Goldbach's conjecture, proposed in 1742 by Christian Goldbach (1690-1764), the Prussian-born number theorist and analyst, in a letter to Leonhard Euler. Goldbach's conjecture states that any even number greater than or equal to 6 can be expressed as the sum of two odd prime numbers (for example, 6 = 3 + 3, 8 = 5 + 3, 48 = 29 + 19). Although there is every reason to believe that this conjecture is true, and computers have been used to verify it for some very large numbers, it has never been proved. Goldbach's conjecture is a good example of the way in which a problem in number theory can be stated very simply yet be very difficult to solve.
Perhaps the most famous problem in number theory is Fermat's last theorem, which defied proof for over three centuries. Pierre de Fermat is often credited with founding modern number theory. Number theory has fascinated amateur mathematicians ever since because so much of the theory of numbers can be understood without a knowledge of higher mathematics.
The positive integers are the numbers 1, 2, 3, … used for counting; they
are also known as the natural numbers. The negatives of these numbers, -1, -2,
-3, … are called the negative integers. Inntegers can also be called signed
numbers or directed numbers.
The set of all positive and negative integers, together with zero, is called the
set of integers and is denoted by Z, from the German word Zahl, which means
number. The set of positive integers, the natural numbers, is denoted by N or by
Z+. The set of positive integers together with zero is called the set of
non-negative integers.
Integers are rational numbers, since any integer can be expressed as a fraction
with a denominator of 1. For example, 3 can be written as 3/1.
Gaussian integers are complex numbers of the form a + bi, where both a and b are
integers. They are named after the German mathematician and astronomer, Karl
Friedrich Gauss. Gaussian integers are particularly useful for factorizing
equations in certain problems. For example, a2 + b2 = (a +
bi)(a - bi).
In 1799 Gauss proved that every algebraic equation has a root that is a Gaussian
integer. Gauss also demonstrated that certain Gaussian integers are
"prime"; they cannot be reduced to a product of other Gaussian
integers.
A prime number is an integer that can be divided only by one and itself. In other words, an integer is a prime number if the only integers that divide it an exact number of times, without leaving a remainder, are one and itself. An integer that is not a prime number is called a composite number.
The Sieve of Eratosthenes is a routine for compiling a table of prime numbers
devised by the Greek mathematician Eratosthenes in the 3rd century BC. It allows
us to find all of the prime numbers less than a given number N.
First we write down all of the numbers less than N (except 1). For example,
suppose we want to find all of the prime numbers less than 49. We write down the
numbers 2 to 48.
We then take the first prime number, which is 2, and cross out all its
multiples. In other words, we cross out every second number, starting with 2 ×
2 = 4. In our example, this will leave us with the set of numbers in Diagram 1.
Diagram 1
We then cross out all the multiples of the next prime number, 3, that remain, starting with 3 × 3 = 9. This leaves us with the numbers in Diagram 2.
Diagram 2
We continue this process, deleting all multiples of the next prime number, until we get to the last prime number before ÖN. In our example, N = 49, so ÖN = 7. Therefore the last prime number for which we need to cross out the multiples is 5 (see Diagram 3).
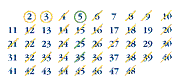
Diagram 3
We are now left with all the prime numbers less than 49, as in Diagram 4.
Diagram 4
We can use this method to find all the prime numbers less than 100 (see Diagram 5).
Diagram 5
The fundamental theorem of arithmetic states that any composite number can be
written as the product of prime numbers, called its prime factors, in one and
only one way (provided that the order of the factors is not taken into account).
For example, 385 = 5 × 7 × 11, but is not equal to the product of any other
set of prime numbers. Some of the prime factors may be repeated factors. For
example 75,900 = 2 × 2 × 3 × 5 × 5 × 11 × 23. This has two repeated factors, 2 and 5.
This theorem means that prime numbers can be regarded as "building
blocks" for the integers. It might seem reasonable to think, therefore,
that there would be some kind of pattern determining which numbers are prime.
However, there is no such pattern.
If we look at the small integers, prime numbers appear to be very common. For
example, half of the numbers 2 to 11 are prime, namely 2, 3, 5, 7, and 11. Of
the next ten numbers, 12 to 21, three are prime (13, 17, and 19), a proportion
of 30 per cent. Of the first thousand integers, 16.8 percent are prime numbers,
while, in the first million integers, 7.85 percent are prime. Therefore it
seems reasonable to suppose that prime numbers become less frequent as numbers
become larger.
The prime number theorem tells us how many prime numbers there are likely to be
that are less than or equal to a certain value n. It states that the proportion
of positive integers less than or equal to n that are prime numbers tends toward
1/lnn as n increases (where lnn is the natural logarithm of
n). Despite this decrease in frequency it is believed (but has never been proved) that there are
an unlimited number of twin primes (pairs of primes that differ by only 2). The
largest known pair of this kind is 242,206,083 × 238,880 + 1 and 242,206,083 ×
238,880 - 1 (each with 11,713 digits). This pair of twin primes was discovered
in November 1995 by Indlekofer and Ja'rai.
There are an infinite number of prime numbers. We can prove this by proving that
there is no largest prime number.
First we suppose that pn is the largest prime number and that p1,
p2, …, pn-1
are all of the prime numbers less than pn. In other words, p1 = 2,
p2 = 3, p3 =
5, etc.
Next we consider the number N formed by multiplying all of the prime numbers up
to pn together and adding 1. In other words,
N = p1 × p2 × … × pn + 1
We can see that the number p1 × p2 × … × pn can be divided exactly by any
of the prime numbers p1 to pn. Therefore, if we try to divide the number N =
p1× p2 × … × pn + 1 by any of the prime numbers p1 to
pn, we will always have a remainder of 1 (the 1 that we added to the product). This means that either N
is a prime number itself or it is divisible by a different prime number (that
must be greater than pn, since all smaller primes fail to divide N exactly). In
either case, we have shown that a prime number bigger than pn exists. This
contradicts our original assumption that pn is the largest prime number, so we
must conclude that there are an infinite number of prime numbers.
Early attempts to find a pattern in the distribution of primes concentrated on
finding an algebraic formula that would always yield a prime number. Marin
Mersenne, a 17th-century French monk, investigated numbers of the form
Mp = 2p - 1
where p is a prime number. Numbers of this form were later called Mersenne
numbers. He stated that these numbers would be primes if p is 2, 3, 5, 7, 13,
17, 19, 31, 67, 127, or 257, and composite numbers for all other values of p
less than 257. It was not possible to check this until 1947 when desktop
calculators became available. Despite making a few mistakes, in general Mersenne
was very accurate.
Mersenne numbers provide a way of producing some spectacularly large prime numbers, such as 2132,049 - 1 (39,751 digits), 2216,091 - 1 (65,050 digits), and 2756,839 - 1 (227,832 digits). In fact, the largest number that has so far been proved to be prime (by Slowinski and Gage in January 1994) is a Mersenne number. This is the number 2859,433 - 1 , which has 258,716 digits.
Two famous theorems concerning prime numbers are: (1) Fermat's theorem that if p is prime and a is a positive integer, then p is a divisor of ap - a; and (2) Wilson's theorem (actually first proved by Joseph Louis Lagrange) that p is prime if and only if p is a divisor of (p - 1)! + 1.
A Diophantine equation is a numerical polynomial equation that has more than
one unknown quantity and integer coefficients, and for which a solution is
sought in integers. For example,
23x + 21y + 7 = 0
is a Diophantine equation, where x and y are the unknown quantities. Famous
examples of Diophantine equations include Pythagoras' theorem and Fermat's last
theorem.
Diophantine equations are named after the Greek mathematician Diophantus of
Alexandria, whose book Arithmetica included a study of such equations.
There are routine methods for solving an equation of the form
ax + by + c = 0
which always has an unlimited number of solutions. For example, the equation
23x + 21y + 7 = 0
has a solution (x = 7, y = -8); however, any pair of integers
(x = 7 - 21t, y = -8 + 23t)
where t is any integer, is also a solution. For example, if we take t as 2, we get the solution
x = 7 - 42 = -35
y = -8 + 46 = 38
There are also routine methods for solving an equation of the form
ax2 + bxy + cy2 + dx + ey + f = 0
(second-degree equations), which may have an unlimited number of solutions, a
finite number of solutions, or no solutions at all, depending on the coefficients a, …, f.
Fermat's last theorem has excited mathematicians for centuries. It is one of the simplest mathematical problems to state, and yet it has proved one of the hardest to solve.
Pierre de Fermat was a 17th century French lawyer and amateur mathematician. He
is often credited with founding modern number theory and he made some of the
greatest advances in the history of mathematics.
In the 3rd century AD the Greek mathematician Diophantus of Alexandria wrote a
book called Arithmetica, in which he proposed a number of mathematics problems.
Fermat had a copy of this book, which he studied. He also made notes in the
margins and it was one of these notes that set mathematicians a puzzle that
lasted for over three centuries.
Fermat considered Pythagoras' theorem, which states that, for every right-angled
triangle, the square of the hypotenuse is equal to the sum of the squares of the
other two sides. This can be rewritten as x2 + y2 = z2. Fermat asked himself
what would happen if, instead of being squared, the numbers were cubed or raised
to the power of 4, 5, or any other higher number. In other words, would it be
possible to find a solution to the equation xn + yn = zn when n is any integer
greater than 2? Fermat concluded that it would not. This is Fermat's last
theorem.
Formally, Fermat's last theorem states that it is impossible to find a nonzero
integer solution to the equation xn + yn = zn if n is any integer greater than
2.
Not only did Fermat state this theorem, but, in the margin of the book, he also
wrote, in Latin, that he had a wonderful proof of it. The note finishes with the
words "Hanc marginis exigiutas non caperet" - this margin is too small
to contain this. So Fermat said he had a proof. Nobody knows if he really did,
but if he ever wrote it down, it was lost.
Many of the greatest mathematicians since have tried, and failed, to prove the
theorem. Then, in 1993, British mathematician Andrew Wiles claimed that he had
at last found a proof. Wiles had worked in complete secrecy for seven years to
produce the proof, and the announcement, made at an international conference,
created an uproar in the mathematical world. Newspapers from around the world
printed stories on the discovery.
Before the proof could be published in a journal it had to be refereed. This
meant that other mathematicians, chosen by the journal, had to go through the
proof line by line to make sure it was completely correct. It took two months,
with the referees contacting Wiles frequently to clarify details. As a result of
this process an error was discovered. At first it seemed a trivial problem,
easily solved, but the more Wiles tried to fix the mistake the worse it became,
until finally it became clear that a fundamental flaw in the proof had been
uncovered.
For a year, Wiles, helped by other mathematicians, tried to repair the proof. On
the point of abandoning it, Wiles went back for one last look at the problem
area. That was when, completely unexpectedly, he realized how the proof could be
made to work. This time, when it was checked, the proof was watertight. The
problem that had baffled mathematicians for over three centuries had been
solved.
However, Wiles' proof could not possibly be the same as the proof Fermat claimed
to have discovered in about 1637. In his proof, which was hundreds of pages
long, Wiles used many mathematical results that have only been discovered since
Fermat's time.
Wiles built on the work of many mathematicians, working at different times in
different places, and used results from a variety of areas of mathematics. His
proof of Fermat's last theorem is likely to be remembered as one of the greatest
ever mathematical achievements.