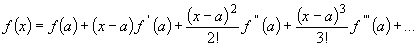Tangents and Normals
Continuity
                Singular Points
Taylor's Theorem

Tangents and Normals

A tangent is a line that touches a curve at a point and has the same gradient as the curve at that point. Diagram 1 shows a tangent to the curve at point P.

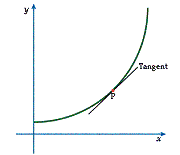
Diagram 1: A Tangent

A normal is a line that is perpendicular (at right angles) to a given line or plane, or to a tangent at the point where it touches the curve. Diagram 2 shows the normal to the tangent.

Diagram 2: A Normal

The gradient of a curve at a point is the same as the gradient of the tangent to the curve at that point. The gradient of the tangent to a curve can be found by differentiation. The gradient of the normal that is perpendicular to the tangent at the point where it touches the curve can be found from the gradient of the tangent. The tangent and the normal are always perpendicular to each other, and it can be shown that the product of their gradients always equals -1. For example, if a tangent has a gradient of 2, the gradient of the normal is given by
                gradient of normal × 2 = -1
So,
                gradient of normal = - ½

Go to top

Continuity

Continuity is a property of functions. In simple terms, a function is continuous if it has an uninterrupted graph. For example, Diagram 1 shows the graph of the continuous function f(x) = x³.

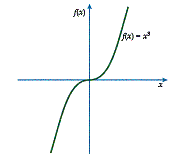
Diagram 1: A Continuous Function

Diagram 2 shows two ways in which a function can be discontinuous. The function
                f (x)=1/x²
is discontinuous at x = 0 because the function is not defined at this point. The function defined by

Go to top

is also discontinuous. Although it is defined at x = 0, it "jumps" at this point.

Diagram 2: Discontinuous Functions

Therefore, both of these functions have a discontinuity at x = 0.
A more formal definition of continuity can be given in terms of limits. A function f(x) is continuous at a point x₀ if the limit of f(x) as x tends to (gets closer to) x₀ is the value of the function at x₀, that is, if

This should hold whether x tends to x₀ from below or above the value of x₀.

Go to top

Singular Points

Some discontinuities are singular points. A singular point of a curve is any point at which the curve does not have a unique tangent. From this, it follows that the function will not be differentiable at a singular point. A singular point of a curve can occur where the curve is pointed, where it crosses itself, or where it branches in two directions. Crossings are called multiple points of the curve. An example of a function with a multiple point is shown in Diagram 3.

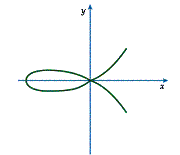
Diagram 3: Multiple Points

Pointed sections of the curve are called cusps of the first kind. An example of a function with a cusp of the first kind is shown in Diagram 4.

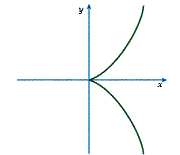
Diagram 4: Cusps of the First Kind

Go to top

A point where a curve branches into two directions is called a cusp of the second kind. An example of a function with a cusp of the second kind is shown in Diagram 5.

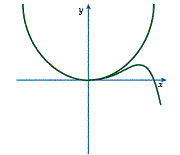
Diagram 5: Cusps of the Second Kind

Singular points sometimes have special significance. In physics, for instance, a black hole is considered to be a singular point in space-time.

Taylor's Theorem

Taylor's theorem provides a way of estimating the values and behaviour of a function near a point just by knowing the value of the function at that point. By knowing how a function behaves near a point it is possible to estimate whether that point is a maximum or minimum. If, for instance, the function represented the speed of a car, Taylor's theorem could be used to decide at which points the car's speed stopped increasing and started decreasing, and vice versa. Taylor's theorem is named after the British mathematician Brook Taylor (1685-1731), who first published it in 1715.
If the value of a function f is known at a point a, then Taylor's theorem provides an approximation of the value of the function at a nearby point, a + h. The value of the function at the point a + h is given by

Go to top

The more terms of the series that are added, the more accurate the approximation of the value of the function at a + h will be. For Taylor's theorem to work, the derivatives of the function must be continuous.
Taylor's theorem can be used to expand some functions as power series. If a function can be expanded in this way, the power series given will be of the form