Angles
Angles Between Lines
Angles NotationDegrees and RadiansBearingsFinding Bearings| home | stands | games | about | mpjournal | back | links |
AnglesAngles Between Lines
Angles NotationDegrees and RadiansBearingsFinding BearingsAngles are formed where two straight lines meet. They can be measured using a protractor or an angle indicator. Angles are measured in units called degrees. A degree is obtained by dividing the circumference of a circle into 360 equal-sized parts. Mathematicians use a small circle (°) as a symbol to indicate degrees. The angle that occurs at the corners of squares and other rectangles is 90° and is called a right angle. Angles of less than 90° are called acute angles. Angles measuring between 90° and 180° are called obtuse angles. Angles measuring between 180° and 360° are called reflex angles. Using a protractor, we can identify an acute angle, a right angle, an obtuse angle, and a reflex angle.
The simplest type of angle is one between two straight lines. This is called a plane rectilinear angle.
Two angles are described as conjugate if they add up to 360° (2p rad). e.g. the conjugate angle of 120° is given by
360° - 120° = 240°
Two angles are described as complementary if they add up to 90° (p/2
rad). e.g. the complementary angle of 30° is given by
90° - 30° = 60°
The two acute angles of a right-angled triangle will always be complementary (see diagram).
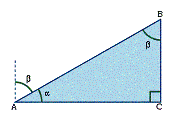
One way to denote an angle between two lines is to use the names of the points at the ends of the lines. For example, the angle a in the above diagram could be written as the angle BĀC. The angle a could also be correctly denoted as the angle at A. Although it is not strictly correct to do so, this is often abbreviated to the angle A. Another way to label an angle is with Greek letters, particularly q.
In everyday life it is usual to measure angles in degrees (abbreviated ° ). 1° is divided into 60 minutes (abbreviated ' ), and each minute is divided into 60 seconds (abbreviated " ). If a circle is drawn with its centre at the vertex of an angle of 1° then the arms of the angle cut off an arc whose length is 1/360 of the circumference of the circle (see diagram).
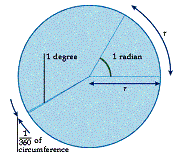
Although degrees are more commonly used, the SI unit for measuring angles is the radian (rad). If a circle is drawn with
its centre at the vertex of an angle of 1 rad then the arc of the circle cut off by the arms of the angle has a length equal to
the radius of the circle (see diagram above). The length of the circumference of a circle of radius r is 2pr. Therefore
2p rad = 360°. So
1 rad = 180/p°
» 57.29578° (to 5 decimal places)
and
1° = p/180 rad
» 0.01745 rad (to 5 decimal places)
So, for example, an angle of 90° is the same as an angle
of p/2 rad, and an angle of 180° is the same as an angle of p rad.
A bearing gives the direction of a line compared to true north or magnetic north. Bearings are three-figure numbers; for example, if you were walking east, you would be walking on a bearing of 090 because the angle between north and east, measured clockwise, is 90°. Compasses often have the bearings for the compass points written round their edges (see Diagram 1).
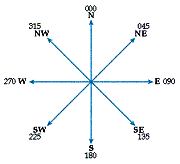
Diagram 1: Bearings of Compass Points
Bearings given relative to true north are called true bearings and bearings given relative to magnetic north are called magnetic bearings. Bearings are particularly used for navigation in ships and airplanes because it is not necessary for any landmarks to be visible for bearings to be used.
To find the bearing of point B from point A, first join the two points together with a straight line. Then mark in the line pointing north at point A and measure the angle clockwise from the north line to the line joining the points. This angle will be the bearing from A to B. For example, the bearing from A to B in Diagram 2 is 040 because the angle from the north line to the line joining A and B is 40°.
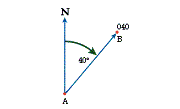
Diagram 2
The bearing from A to B is not the same as the bearing from B to A because bearings are always measured clockwise from the north line. Thus the bearing from B to A in this example is 220 (see Diagram 3).
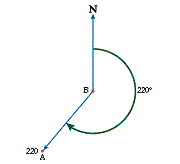
Diagram 3
In this case, the bearing from B to A is the bearing from A to B plus 180°. In general, if the bearing from A to B is known, then the bearing from B to A can be found by either adding 180° to the bearing from A to B, or subtracting 180° from it. A bearing is always less than 360, so it should be obvious whether adding or subtracting will give the correct reverse bearing.