home stands games about mpjournal back links
Euler's Formula
            Euler's Formula for Polyhedra    Proving Euler's Formula
Surfaces
            Planes    Spheres    Cylinders    Pyramids

Solid Figures

Mathematicians have puzzled for centuries over the properties of solid figures. The solid figures most easily categorized are called polyhedra. Only five regular polyhedra exist. Called the Platonic solids, they are the tetrahedron (four triangular faces), the cube (six square faces), the octahedron (eight triangular faces), the dodecahedron (12 five-sided faces), and the icosahedron (20 triangular faces).

Euler's Formula

The Swiss mathematician Leonhard Euler proposed and proved a very useful result about networks, which is now called Euler's formula. This formula can very easily be applied to polyhedra.
Euler's formula is true for a network if, for all points in the network, we can get to any other point in the network along connecting paths. (This means that we do not need to think here about "odd" examples of networks, such as a group of points with no connecting paths.)
Any network of this type consists of a number of vertices (points or nodes) joined together by a number of edges (paths or arcs). A region enclosed by edges is called a face (see Diagram 1).


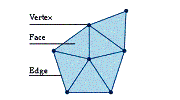
Diagram 1: A Network

Euler showed that, for any network of this type,
            number of vertices - number of edges + number of faces = 1
which can also be written as
            V - E + F = 1
We can see this is true for the example in Diagram 1, which has 7 vertices, 12 edges, and 6 faces. Therefore,
            V - E + F = 7 - 12 + 6 = 1

Go to top

Euler's Formula for Polyhedra

For any polyhedron,
            V - E + F = 2
This is essentially the same result as the one stated above. We can see this by taking any polyhedron, removing one of its faces and stretching it out to lie flat. The edges of the polyhedron will then form the edges of a network with the same number of edges and vertices as the polyhedron, but with one less face. For this network
            V - E + F = 1
Adding back the face we removed will increase F by 1, and hence will give us
            V - E + F = 2
for the polyhedron.
For example, suppose we look at an octahedron. Removing one face and flattening it out gives us the network in Diagram 2.


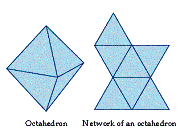
Diagram 2: Euler's Formula for Polyhedra

An octahedron has 6 vertices, 12 edges, and 8 faces. Therefore
            V - E + F = 6 - 12 + 8 = 2
The resulting network has 9 vertices, 15 edges, and 7 faces. Therefore
            V - E + F = 9 - 15 + 7 = 1

Go to top

Proving Euler's Formula

To prove Euler's formula, suppose we start with some network and wish to prove that V - E + F = 1. If we remove an outside edge from the network (assuming that it has one), the number of edges in the network will decrease by one, but so will the number of faces, while the number of vertices remains the same. Therefore, the value of V - E + F will also remain the same.
For instance, we can see that this is true for our example above (see Diagram 3).


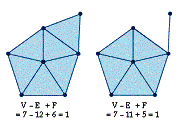
Diagram 3: Removing an Outside Edge from a Network

After removing an outside edge, V = 7, E = 11, and F = 5; therefore
            V - E + F = 7 - 11 + 5 = 1
Alternatively, if the network has a vertex connected to the network by only one edge and we remove both this vertex and the connecting edge, then V and E both decrease by one, while F remains unchanged. Again, this means that the value of V - E + F will remain unchanged.
Again, we can see that this is true for an example (see Diagram 4).


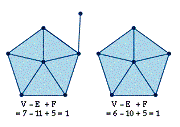
Diagram 4: Removing a Lone Vertex and Connecting Edge from a Network

Go to top

After removing the lone vertex and connecting edge, V = 6, E = 10, and F = 5; therefore
            V - E + F = 6 - 10 + 5 = 1
Now, if we keep carrying out these two operations, removing an outside edge and removing a lone vertex and connecting edge, on our network whenever possible, we will eventually be left with only a single vertex. For this vertex, V = 1, E = 0, and F = 0 and therefore
            V - E + F = 1 - 0 + 0 = 1
Since neither of the operations we have carried out on our original network changes the value of V - E + F, then it must also be true for our original network that V - E + F = 1 and therefore Euler's formula is correct.

Surfaces

The mathematical notion of a surface is very general, but is based on the simple intuition of a surface in the physical world. Informally, we speak of the surfaces of solid objects: for example, "the surface of a table is flat", or "the surface of a ball is round", or "the ball is touching the surface of the table". From these sentences we can see that our informal notion of a surface is that it represents some sort of boundary between an object and its surroundings and that it can have geometric properties independent of its surroundings. For instance, a triangle on the surface of a ball has angles adding up to more than 180 degrees. Also, the surface of a three-dimensional object, such as a table or ball, is itself two-dimensional.
The formal notion of a surface in mathematics is based on such three-dimensional intuitions. In particular, a surface in Euclidean three-dimensional space has two dimensions, though its geometry need not be Euclidean. One reason for studying such surfaces is that they can have their own geometry, independent of the surrounding space, while also being quite simple objects. Therefore, they can be used to study unusual geometries embedded in a more straightforward geometry. The notion of a surface is not restricted to two-dimensional surfaces in three-dimensional spaces. A cube is a three-dimensional surface in four-dimensional space, in fact in any space of dimension greater than three. However, only surfaces in three-dimensional space are considered here. Some of the most commonly encountered surfaces are planes, and spherical and cylindrical surfaces.

Go to top

Planes

A plane is a flat surface such as a tabletop or wall. Any line joining two points in a plane will lie completely on its surface.
The position of any point in three-dimensional space can be specified by giving its Cartesian co-ordinates, (x, y, z). For example, the position of the point in Diagram 1 is given by the co-ordinates (4, 5, 3).


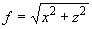
Diagram 1

Go to top

A plane can be specified by an equation in terms of x, y, and z. Any point that has x, y, and z co-ordinates that satisfy the equation will lie in the plane. For example, the equation z = 0 specifies a horizontal tabletop-like surface, and the equation x = z specifies the plane in Diagram 2. All the points in this plane will have x and z co-ordinates equal to each other.


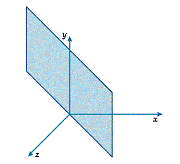
Diagram 2
This plane satisfies the equation x = z.

Most planes have more complicated equations than this. The general equation of a plane is usually given in terms of a normal vector to the plane. A normal line or vector is one that is perpendicular (at right angles) to the plane (see Diagram 3).


Diagram 3: Normal Vector to a Plane

Go to top

The general equation of a plane is ax + by + cz = d where

is a normal vector to the plane. The equation of the plane in Diagram 2 can be given in this form as
            1x + by + (-1)z = 0
where the vector

is normal to the plane, and b can be any number.

Spheres

An example of a spherical surface is the surface of a ball. Every point on a spherical surface is equidistant (equally distant) from the centre of the sphere. The equation of the surface of a sphere centred at the Cartesian co-ordinates (0, 0, 0) is
            x2 + y2 + z2 = r2
where r is the radius of the sphere.
It is easier to see how this equation is derived if the equation of a circle centred at (0, 0) is considered first (see Diagram 4).

Go to top


Diagram 4

The radius, r, is, by definition, the distance between any point (x, y) on the circle and the centre of the circle. However, we can also find this distance in terms of x and y by using Pythagoras' theorem. From Diagram 4 it can be seen that the distance is the same as

In other words,

or
            r2 = x2 + y2
This is the equation of the circle centred at (0, 0).
This concept can now be extended to three dimensions. Imagine that the point (x, y, z) is on a sphere centred at (0, 0, 0).

Go to top


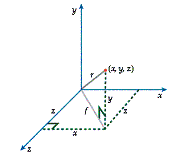
Diagram 5

From Diagram 5, it can be seen that

by Pythagoras' theorem. But f is part of another right-angled triangle and therefore

So

or
            r2 = x2 + y2 + z2
The general equation of the surface of a sphere centred at (a, b, c) is
            r2 = (x - a)2 + (y - b)2 + (z - c)2

Go to top
Surface Area

The surface area of a sphere of radius r is given by 4pr2.

Cylinders

An example of a cylindrical surface is shown in Diagram 6.


Diagram 6: A Cylinder

The equation of the surface of a cylinder is a bit more difficult to work out because there are essentially two types of point on a cylindrical surface, those on the ends of the cylinder and those on the curved surface.
Suppose that the base of the cylinder is the circle in the xy-plane centred around (0, 0, 0) and the height of the cylinder is h, as in Diagram 7.

Go to top


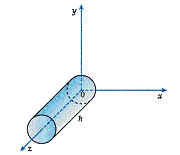
Diagram 7

The equation of the circle around the edge of the base is x2 + y2 = r2. Any point on the base will be on or within this circle and so the distance between the point and the centre will be less than or equal to r. Hence all the points on the base will satisfy the inequality
            x2 + y2 £ r2
All the points on the base have a z co-ordinate of 0, so the equation of the points on the base is given as
            x2 + y2 £ r2, z = 0
The points on the other end of the cylinder have the equation
            x2 + y2 £ r2, z = h
The points on the curved surface of the cylinder can be thought of as being on the edge of a circle because any cross-section through the cylinder will be a circle. Therefore all the points on the curved surface of a cylinder will satisfy x2 + y2 = r2 and their z co-ordinates will be between 0 and h. Hence,
            x2 + y2 = r2, 0 < z < h
Therefore the equation of the surface of a cylinder with its base in the xy-plane centred at (0, 0, 0) is given by
            x2 + y2 £ r2 if z = 0 or z = h
            x2 + y2 = r2 if 0 < z < h
The general equation of the surface of a cylinder with its base in the xy-plane centred at (a, b) and at z = c is given by
            (x - a)2 + (y - b)2 £ r2 if z = c or z = c + h
            (x - a)2 + (y - b)2 = r2 if c < z < c + h

Go to top
Surface Area

The area of the curved surface of a cylinder of radius r and height h is given by the circumference of the circular base multiplied by the height of the cylinder. In other words, the surface area of the curved surface is given by 2prh. The surface area of each end of the cylinder is the area of a circle, pr2. Therefore, the surface area of the whole cylinder is given by 2pr2 + 2prh.

Pyramids

Pyramids are solid figures with triangular sides that meet at the top. Egyptian pyramids have a square base and are called square-based pyramids. The cross-section of a pyramid with a square base is square. It is made by cutting a slice through the pyramid that is parallel to the base.
Tetrahedra resemble pyramids but have four triangular faces of equal size, including the base, and a triangular cross-section. (Cutting a slice through this pyramid parallel to its base gives a square cross-section.)