Higher Dimensions
            Four-dimensional Space-Time    Visualizing Space-Time    Higher Spatial Dimensions    
            Extending the Co-ordinate System    Viewing Higher Dimensions
            What Is Dimension?    What Use Are Eleven Dimensions?

Higher Dimensions

Since the popularization of Einstein's theory of relativity, it has become commonplace to describe our Universe as being four-dimensional. Exactly what does this mean? And what do mathematicians and physicists mean when they talk about five, six, and even eleven dimensions?

Four-dimensional Space-Time

Einstein's model of the Universe uses a theory of four-dimensional space-time first postulated by the Lithuanian mathematician, Hermann Minkowski. Minkowski developed his space-time continuum by joining the three dimensions of space to one-dimensional time. The metaphor commonly used to describe time is that of a one-dimensional object - a line. Linear time consists of a line which stretches into the past in one direction, and into the future in the other. Each present moment is one point on the line (see Diagram 1).

Diagram 1

Minkowski applied this metaphor much more stringently, so that in his model of the space-time continuum, we can measure distances along a time axis just as we might measure them along the x-, y-, and z-axes in Cartesian co-ordinates. The continuum has four mutually perpendicular axes - x, y, z, and t (or time). Before trying to understand exactly how it is possible to have four mutually perpendicular axes, it is worthwhile considering how the abstract idea of four-dimensional space-time corresponds to the world as we experience it.
We are accustomed to perceiving a three-dimensional world, populated with objects that have length, width, and height, and a location in space given in terms of these three independent measures. From experience, then, the Universe appears to be three-dimensional. However, it can be argued that in order to experience anything, that thing has to endure - it has to exist in successive moments in time. (The person who experiences must also endure in time). Having identified that an object's existence is bound up with its existence at particular points in time, an obvious next step is to try and locate its position in both space and time. For example, we might locate the position of a person in space-time by giving their spatial co-ordinates and the corresponding time co-ordinates for each moment of their life. These co-ordinates would be given relative to some origin in space (such as the Earth's north pole), and also relative to some fixed point in time (such as the birth of Jesus Christ). So we might say that this person existed at these successive points (or co-ordinates) in space and time, beginning with their place and date of birth and ending with their place and date of death. If we construct our co-ordinate system so that the origin in space coincides with the origin in time, we end up with a model of the space-time continuum.

Go to top

Visualizing Space-Time

By limiting the number of spatial dimensions allowed to just one, we can add the dimension of time and still be able to construct a simple model that can be visualized. If the person is constrained to move in only the x-direction, we can add a t-axis (representing time) where we would normally place the y-axis. This person's existence can then be plotted as a set of points in two-dimensional space-time (see Diagram 2).

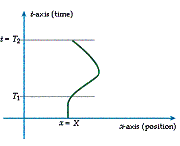
Diagram 2

The points all lie on a curve through two-dimensional space that describes completely their location. If we now remove the constraints on movement, and allow the person to move in all three spatial dimensions, the set of points that completely describes their location lies on a curve through four dimensions - and here lies a real difficulty. Any static visualization of Minkowski's space-time continuum treats time as, effectively, a fourth spatial dimension. We might accept that complete positional location requires both spatial and temporal co-ordinates, but where in the Cartesian co-ordinate system do we fit in a fourth independent axis? And we need not stop at four - some physicists postulate that the Universe really is eleven-dimensional, and there are mathematicians who work in even higher dimensions.

Go to top

Higher Spatial Dimensions

The idea of a geometrical system with more than three spatial dimensions predates both Minkowski and Einstein; it is to these earlier, purely mathematical constructions that we now turn. The abstract mathematical constructions are basically generalizations of the geometry that we learn at school - the everyday geometry that organizes (or perhaps, is organized by) our simple spatial intuitions, namely that objects can have length, width, and height. Any point in space can be identified by its position relative to a known starting point, called the "origin". Identifying the position of a point P relative to the origin O can be done in terms of distances in three directions: the distance that P is forward or backward from O, the distance that P is left or right of O, and the distance that P is above or below O. Each of these three directions is at right angles to the other two (they are mutually perpendicular), so it is possible to move P in one direction without affecting the other two distances from O (that is, each direction is independent of the other two; see Diagram 3).

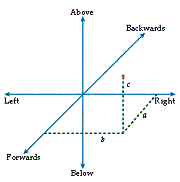
Diagram 3

If P moves (changes position), then the new position, and the velocity and acceleration during the move, can also be described along these three directions. The three independent and mutually perpendicular directions, or axes, along which we make measurements are called dimensions. This is an informal explanation of what "dimension" means, and of what it means for space to be three-dimensional.
To specify the position of a point in a two-dimensional space requires distances to be measured along only two axes. For example, any point on the surface of a flat sheet of paper can be located by its distance from a fixed origin in each of two directions: across the page, and up or down the page. The surface of a piece of paper is thus a two-dimensional space. What is the dimension of a line drawn on such a piece of paper? Take a point on the line as the origin O, then any other point P can be given by stating the distance traveled along the line from O to P, where a negative distance means "traveling in the opposite direction". So a line on the paper is a one-dimensional object (see Diagram 4).

Go to top

Diagram 4

Extending the Co-ordinate System

Using co-ordinate geometry, we can summarize the distances of a point P from the origin by giving its position vector. For example, the flat surface of an infinite plane can be represented by a two-dimensional co-ordinate system: each point on the plane is identified by a pair of co-ordinates x and y, or in vector notation, (x y). This point can be reached from the origin (0, 0) by traveling x units in the x-direction along the x-axis, and y units in the y-direction along the y-axis (see Diagram 5).

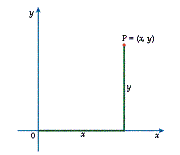
Diagram 5

Go to top

It is easy enough to imagine another direction, the z-direction, at right angles to the other two. A graph of such a three-dimensional space would have a z-axis pointing up out of the page. In the three-dimensional space that we inhabit, a point would be located using a position vector of the form (x y z). Following the pattern between the number of dimensions and the number of elements required in the position vector, we can conceive of a co-ordinate system for four dimensions where a point is located by the vector: (w x y z). In general, an N-dimensional co-ordinate geometry is a space in which N different quantities are required to identify a point relative to a fixed origin. Visualizing such spaces of four or more dimensions is not so straightforward - the whole point of co-ordinate systems is to avoid the need for such visualization by using algebra instead of graphs.
The great utility of co-ordinate geometry lies in the fact that, once we have defined an N-dimensional space, we can apply many simple geometrical results from spaces of other dimensions, with only slight modifications. For example, the equation
            x² + y² = r²
describes a circle of radius r in two dimensions. In three dimensions, the equation for the corresponding figure, a sphere of radius r, is:
            x² + y² + z² = r²
The move into four dimensions is straightforward too, as long as we do not depend on a "mental image" to confirm the algebra.
            w² + x² + y² + z² = r²
is the equation of a four-dimensional sphere (a 4-sphere, or hypersphere) of radius r.

Go to top

Viewing Higher Dimensions

"Seeing" four-dimensional figures directly is (for our present minds, anyway) just not possible. In fact, "seeing" in two-dimensions is probably as difficult. Squares and circles seem familiar enough, but it is worth remembering that we generally encounter them only in our three-dimensional space - a square drawn on a sheet of paper is, on a microscopic level, three-dimensional (the paper, and the layer of pencil graphite on it both have thickness), whereas the geometrical figure has zero thickness. If we turn the sheet of paper edge-on to us, we perceive its thickness (though perhaps not that of the graphite). A "real" two-dimensional object seen edge-on would simply disappear! In the example just discussed, we were looking down onto a two-dimensional figure from a viewpoint in three dimensions. But what do squares and circles look like from within a two-dimensional world? As Edwin. A. Abbott's book Flatland, published in 1884, describes, such figures would appear, to a person living in two-dimensions (a "flatlander"), to be nothing more than lines. Furthermore, as a line segment is turned end-on to a flatlander, it disappears, just as a two-dimensional figure does when viewed edge-on by a three-dimensional observer! Abbott's effort to show us a two-dimensional world was valiant, but by no means completely successful. Given the difficulties of viewing even two dimensions properly, what hope have we of ever picturing four or more dimensions?
Fortunately, there are two well-established methods for viewing four-dimensional figures indirectly - either via their shadows in three or two dimensions, or by slicing them into three-dimensional pieces. The first method, called projection, is a particularly important type of geometrical transformation. The shadow of a tree on the ground is a projection of a three-dimensional object (the tree) onto the two-dimensional surface of the ground. Projections preserve certain properties of the original figures - for example, whether the figure has a smooth or irregular boundary - while affecting others - such as the size of the figure. The direction of the projection is the direction of the light causing the shadow. Diagram 6 shows three different projections into two dimensions of a three-dimensional cube (or 3-cube) with transparent faces.

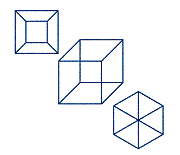
Diagram 6

Go to top

Just as the projection of a 3-cube changes depending on the position of the light source relative to the figure, so too does the projection of a four-dimensional cube (or 4-cube) into three dimensions. In one orientation, the projected figure in three dimensions would be a cube nested inside another cube, their vertices connected by lines. (Note the analogy with the projection of the 3-cube, which is a square within a square.) This projection into three-dimensions can itself be projected into two dimensions - Diagram 7 shows three different projections into two dimensions of a 4-cube.

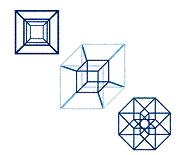
Diagram 7

The other common method of viewing a higher-dimensional figure is by slicing it into cross-sections. (Just as the cross-section of a three-dimensional figure is two-dimensional, so that of a four-dimensional figure is three-dimensional.) A 3-sphere passing through the plane of Flatland intersects it at a point, and then in a circle whose radius increases to a maximum before decreasing to a point, just before the sphere leaves the plane. Analogously, a 4-sphere passing through our three dimensions would appear first as a point, then as a 3-sphere whose radius increased to a maximum before decreasing again to zero.

Go to top

What Is Dimension?

There is an important difficulty with the explanation of dimension given above. It is theoretically possible, though practically ridiculous, to draw a line that completely covers the two-dimensional surface of a sheet of paper, without crossing itself. Such a line is called a space-filling curve, and is sometimes given as an example of complexity in popular books on chaos theory. Though the mathematical existence of such lines in two-dimensional space does not trouble people locating points on pieces of paper, it is of some annoyance to mathematicians, because such a line can be used to identify any point of a two-dimensional space using only one quantity. So it appears that what we thought of as a two-dimensional space might actually be one-dimensional. This confused mathematicians for a long time, since they all wanted a definition of dimension that was consistent with our basic intuitions about positioning points in space. It was not until 1902 that the first really suitable definition of dimension was given, using topology and recursion, by Jules Henri Poincaré. We shall not describe Poincaré's definition, since our informal explanation of dimension suffices here. But we should note that there are several different conceptions of dimension in mathematics. For example, in fractal geometry, dimension can be a fractional number: a space-filling curve on a two-dimensional surface will have a dimension of between one and two. In the theory of vector spaces, the dimension of a space is a whole number N, equal to the number of co-ordinates required to specify a vector uniquely.

Go to top

What Use Are Eleven Dimensions?

Physicists might claim that there really are five, six, or eleven dimensions to our Universe - the reason we feel intuitively at home in only three is that the other dimensions are bundled too tightly for us to notice. At the usual human scales of energy they are just not perceptible, but at the high energies available in particle accelerators, the Universe reveals its higher dimensions. If dimensionality is an inherent property of the Universe, and not just a concept that humans use to understand it, then it is imperative for mathematicians and physicists that they investigate this dimensionality. However, even if we regard the language of dimension as metaphorical, with nothing "real" to correspond to, it is of great utility to mathematicians. The ability to manipulate figures in more than three dimensions is essential to the mathematical modeling of a wide range of systems. We have already mentioned how, in an N-dimensional space, a vector with N elements is needed to identify a point. Mathematicians routinely use vectors with four, five, and many more elements to model systems. For example, the problem of guiding a five-jointed robot arm to perform various tasks can be translated into a problem of finding vector paths in five-dimensional space, and the phase portraits of even quite simple dynamic systems, such as a pair of linked pendulums, may twist and curve through four or more dimensions. So despite initially appearing to be very esoteric, the mathematical study of higher dimensions has very practical applications.