| home | stands | games | about | mpjournal | back | links |
A set or class is a collection of distinct numbers or items. For example, we can define a set S of all stringed instruments. The item v, viola, is a member or element of S (vÎS), but t, trombone, is not (tÏS). Every member of S is also a member of M, the set of all musical instruments, so S is called a subset of M (SÌM). The set of all non-members of M is called the complement of M (M¢). Given another set I, Indian instruments, the union of I and S, IÈS, is the set of those members that belong either to I, or to S, or to both. The intersection of I and S, IÇS, is the set of only those members that belong to both I and S. A set without any members is called the null or empty set (Ø). The set of musical instruments is a subset of the universal set, written e.
We can use letters to represent mathematical sets and their elements, and symbols to represent relationships between sets. The combinations of letters and symbols constitute an algebra of sets. Statements about sets made in this system of algebra follow the rules devised by George Boole, so the system is called Boolean set algebra, or simply Boolean algebra. Since Boolean algebra has only a few basic symbols, even quite simple logical relationships between sets can look quite daunting when translated into this system. As is often the case in mathematics, the situation becomes much clearer if we draw a picture. The English logician John Venn introduced a pictorial representation of set algebra called the Venn diagram, which is simple enough for a young child to understand. Boolean set algebra is isomorphic to (in one-to-one correspondence with) propositional calculus, so Venn diagrams may be used to represent both relationships between sets, and relationships between propositions.
A Venn diagram represents sets topologically, using intersecting circles. In the Venn diagram below, the outer rectangle represents the universal set, e, which includes everything. The definition of a universal set is actually a little more subtle than this, since by Russell's paradox, it cannot include itself. The circle F represents the set F of animals with fur - every animal that has fur will be placed somewhere within F. The circle T represents the set T of animals with tails, and the circle W represents the set W of animals that live in water.
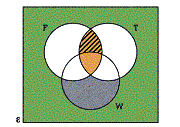
Diagram 1: A Venn Diagram
The tiger has fur and a tail, and so belongs to both set F and set T. The region inside both circles F and T, here coloured orange, represents the intersection of the sets F and T, FÇT. So the tiger belongs in this orange region. However, the tiger does not live in water, so it must be placed outside set W. The tiger is therefore placed in the region inside both F and T, but outside W - in the orange region with stripes, which in set-theoretic notation represents everything outside W but inside both F and T, W¢Ç(FÇT). The octopus has neither fur nor a tail, but does live in water, so it belongs to that region outside both F and T, but inside W - in set-theoretic notation, (FÈT)¢ÇW, which is shaded purple in the diagram. Butterflies have neither fur nor tails, and do not live in water, so they belong to the region outside F, T, and W, but inside the universal set e - in set-theoretic notation, in the region ((FÈT)ÈW)¢ (coloured green).
The idea of a set is easily grasped, at least initially. A set is just a neat way of organizing items - it is a mathematical filing system. Many mathematicians have attempted to organize all of mathematics by using sets to determine the basic patterns and relations. But if sets are to provide such a foundation for mathematics, then what provides the foundations for the idea of sets? A formal analysis of sets leads to numerous complications, paradoxes, and counterintuitive results. Even determining how big a set is not always a straightforward task. Set theory has developed out of attempts to understand this and similar very general problems, and has had a profound impact on concepts of classification, counting, and the infinite.
Consider the set N = {0, 1, 2, 3, … } of natural numbers, and the set E = {0, 2, 4, 6, … } of even natural numbers. On the one hand, it appears as if E has only half as many elements as N, but on the other, both sets seem to contain an infinite number of elements. An analogous problem had been noticed by Galileo Galilei in the early 17th century, but it was 250 years later that George Cantor, the founder of set theory, discovered a solution. Cantor's work on infinite sets relies on the concepts of mappings and cardinality.
A mapping from a set S to another set T takes each element of S and assigns an element T to it. This is written f: S®T. The mapping may assign many different elements of S to the same element of T (a many-one mapping), or it may assign each element of S to a unique element of T (a one-one mapping).
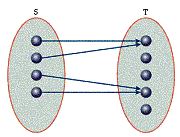
Diagram 1: Many-One Mapping
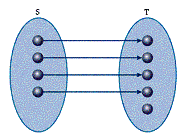
Diagram 2: One-One Mapping
If there is a one-one mapping f: S®T then T must have at least as many elements
as S. We say that the cardinality (the number of elements) of S is less than or
equal to the cardinality of T (written |S| £ |T|). It can also be shown,
although it is not as easy as it seems, that if |S| £ |T| and |T|
£ |S| then the sets are of the same size (|S| = |T|), and we say that S and T are in
one-one correspondence, or bijection. If S is finite, we can find its
cardinality simply by counting its elements. This amounts to finding the set N =
{1, 2, 3, … , n} that is in one-one correspondence with S; that is, finding
one-one mappings f: N®S and g: S®N. Then, |S| = |N| = n.
If a set S consists only of elements of set T, then S is called a subset of T
(written SÌT). For example, both the sets {1, 3} and {1, 2, 3} are subsets of
the set T = {1, 2, 3}. There is an obvious one-one mapping (called an
inclusion), i: S®T, that maps each element of S onto itself as an element of T.
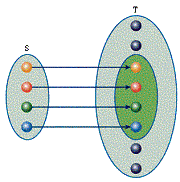
Diagram 3: Inclusion Mapping
S is called a proper subset of T if it does not include all the elements of T, so S={1, 3} is a proper subset of T = {1, 2, 3}, while S = {1, 2, 3} is not.
The set of all the subsets of T is called the power set of T, Ã(T) . For finite sets, |Ã(T)| = 2|T|. This is because, for each element xÎT and each subset SÌT, there are two possibilities: either xÎS or xÏS. Given |T| elements, each of which may be included or excluded from S, there are 2|T| combinations of elements, and therefore 2|T| different subsets S. For example, suppose T = {1, 2, 3}. T has 3 elements, and Ã(T) = {Æ, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}} has 23 = 8 elements. Note that both the empty set, Æ, and T itself are elements of Ã(T). Cantor was able to prove that, in general, |Ã(T)| > |T|.
Amid much controversy, Cantor produced a theory of infinite sets that resolved the original problem concerning the natural numbers, N = {0, 1, 2, 3, … }, and the even naturals, E = {0, 2, 4, 6, … }. E is a subset of N since every element of E is also an element of N, so there exists a one-one inclusion mapping i: E®N, and |E| £ |N|. But we can also define a one-one mapping (×2): N®E, which simply doubles each element of N, taking each natural number n to 2n. Thus, |N| £ |E| too, so combining this with the previous result, |N| = |E|. The two sets have the same cardinality - they are of the same size. An infinite set may actually be defined in this way, as a set that can be put into a one-one correspondence with a proper subset of itself. A set such as E that can be put into one-one correspondence with N, the set of natural numbers, is called countably or denumerably infinite, and its cardinality is denoted by the symbol |N| = À0 (or À-null, aleph-null).
Following the analogy with finite sets, we would expect the set of all subsets of the natural numbers, Ã(N), to have cardinality 2À-null - but what could this mean? Above, we stated that the cardinality of the power set is strictly greater than that of the set itself, but it is a little difficult to see how 2À-null could be greater than À-null (infinity). Surely anything "greater than" infinity is simply infinity, too? Cantor devised an ingenious method called the diagonal argument to show that 2À-null > À0 is indeed true - so there exist at least two different infinities.
The basic form of Cantor's diagonal argument can be stated quite simply.
Consider the set I of all strings that consist solely of 0s and 1s. The strings
may be of finite or infinite length. A typical element of I would look like
0010111010100. . . . In general, each element can be written as a string a0a1a2a3a4a5… , where each an
represents 0 or 1. The set I can be put in
one-one correspondence with Ã(N) using the mapping that takes a string
a0a1a2a3a4a5… to the set
SÌN defined by S={nÎN: an = 1}. The "typical
element" 0010111010100… of I (above) would correspond to S =
{2,4,5,6,8,10, … } of N, while the set EÌN would correspond to the element
101010101010… of I. Because there exists a one-one correspondence, |I| = |Ã(N)|
= 2À-null.
Now suppose that a one-one correspondence exists between I and N, so that I is
countably infinite. Then, it would be the case that À0 =
2À-null. Such a
one-one correspondence between I and N could be written as follows, counting out
the elements of I using the natural numbers and indicating the nth element of I
using the notation an0an1an2an3an4an5… :
| n | element of N |
| 0 | a00a01a02a03a04a05… |
| 1 | a10a11a12a13a14a15… |
| 2 | a20a21a22a23a24a25… |
| 3 | a30a31a32a33a34a35… |
| 4 | a40a41a42a43a44a45… |
| … | … |
Such a list supposedly includes every element of I (and of N). However, Cantor showed that it is always possible to make a new string, not included in the list, that would be an element of I. He created the new string from the diagonal number of the list. The diagonal number d0d1d2d3d4d5… is formed by taking numbers diagonally down the list (a00a11a22a33a44a55… ), and by changing each digit to a0 if it is a1, and to a1 if it is a0. For each n, then, dn ¹ ann. The string d0d1d2d3d4d5… cannot be anywhere in the list: not in the 0th row, because d0 ¹ a00; nor in the 1st row, because d1 ¹ a11; nor in the nth row for any value of n. Cantor concluded that 2À-null > À0 - the elements of the set I cannot be counted with the natural numbers. The cardinality of sets such as I is an uncountable infinity, which is not the same as the countable À0. This was the first step in Cantor's foundation of transfinite arithmetic - the arithmetic of infinite numbers.
Towards the end of the 19th century, Georg Cantor, Gottlob Frege, and other mathematicians did a great deal of meticulous work in set theory in the hope that it would provide a firm foundation for both mathematics and philosophical argument. To this end, Frege began writing a multi-volume treatise, Grundgesetze der Arithmetik (The Basic Laws of Arithmetic). In 1902, as the second volume of Frege's work was on the press, he received a letter from the English philosopher and mathematician, Bertrand Russell. Russell praised the book very highly, but added "There is just one point where I have encountered a difficulty." This "one point" turned out to be the paradox which shook the foundations of logic, and prompted a turn away from the intuitive set theory of Cantor to a more restricted axiomatic theory.
Russell's paradox may be formulated in several equivalent ways. Classically, it
is known as the Barber paradox: every man in Seville is shaved by the barber of
Seville, if and only if he does not shave himself. Does the man who is the
barber shave himself?
If the man who is the barber does not shave himself, then he is shaved by the
barber, who is himself, so he does shave himself. Yet if the barber does shave
himself, then he is shaved by the barber, but according to the statement the
barber only shaves those who do not shave themselves, so he does not shave
himself. No matter how we approach the question, the result is
self-contradictory.
The paradox may be expressed in set theoretic terms. According to Cantor's set
theory, a set is simply a collection of elements of some kind. The elements that
a set contains may be other sets, and a set may even contain itself. For
example, the set of mathematical ideas is itself a mathematical idea, so it
contains itself. Russell considered a set X defined by the fact that X does not
contain itself, and the set Y of all sets X.
Y={X: XÏX}
Russell then asked if Y contains itself. If it does, then since all sets
contained in Y are sets that by definition do not contain themselves, Y cannot
contain itself. If, on the other hand, Y does not contain itself, then it
satisfies the definition for inclusion in Y, and so it does contain itself. If YÎY, then
YÏY, which is a contradiction; but if YÏY, then
YÎY, which is also
a contradiction.
There is another well-known paradox, devised by the German mathematician Kurt
Grelling, that might appear to be of the same type as Russell's paradox.
Grelling defined the adjective "heterological" to mean
"non-self-descriptive". "Polysyllabic" is a polysyllabic
word (it is self-descriptive) so it is not heterological, whereas
"monosyllabic" is not monosyllabic (it is not self-descriptive) so it
is heterological. The question is, then, if "heterological" is itself
heterological. If it is, then it describes itself, so it is not; but if it is
not, then it is non-self-descriptive, so it is!
Grelling's paradox and Russell's paradox are usually considered to be of
distinct types, although the distinction is subtle and contested. Grelling's
paradox is a semantic paradox - a paradox of linguistic meaning - that is best
resolved by considering a hierarchy of languages as proposed by the logician
Alfred Tarski (1902-). In contrast, Russell's paradox is not a paradox of
semantics but one of set theory, and the appropriate resolution is Russell's own
"theory of types".
Paradoxes pose a particular problem for mathematicians because of the
contradictions that they embody. For those mathematicians like Frege and Russell
who attempted to create a foundation for mathematics out of the laws of logic,
any contradictions found in logically valid arguments would bring into question
the validity of the entire system of logic, and hence of mathematics. It was
thus imperative for Russell to remove the paradox from set theory, and he
attempted to do this through his theory of types.
Russell's resolution of his paradox was through his assertion of a hierarchical
set theory. According to this theory of types, sets occur in types, and a set of
a particular type can only contain sets of a lower type. A set of the lowest
type cannot have any sets as elements, only nonsets, while a set of the next
highest type may contain both nonsets and sets of the lowest type. No set can
include itself as an element, because it would then contain a set of the same
type, so the formation of the set Y of all sets that do not contain themselves
is simply not allowed. Although it prevents the occurrence of the paradox,
Russell's theory of types has proved to be insufficient to rescue his project of
logicism.
An alternative approach to logicism was that taken by David Hilbert, Ernst
Zermelo (1871-1953), and others . These mathematicians drew up formal
collections of rules and axioms, which would be strong enough to prevent
paradoxes from occurring while allowing the theorems of mathematics to be
derived. This approach, called formalism, is not concerned with the meaning of
mathematics, only with its consistency and completeness. Although Zermelo's
axioms remain one accepted basis for set theory, the programme of formalism
suffered severe blows in the 1930s, when Kurt Gödel proved the incompleteness
of all formal systems, and again in the 1960s, when Paul Cohen showed that in
formal systems, the truth or falsity of some important mathematical theorems was
simply undecidable.
During the early years of the 20th century, many mathematicians and logicians
were engaged in an attempt to understand the related disciplines of logic,
arithmetic, and set theory in a formalized manner. The formalist programme, led
by David Hilbert, was motivated by the belief that when translated into a formal
system or language, these disciplines would be shown to be both consistent (free
of contradiction), and complete (powerful enough to prove the truth, or falsity,
of all relevant statements). The standardly accepted system of logic (the
first-order predicate calculus) was known to be consistent, and in 1930 Kurt
Gödel proved that it was also complete. Gödel then turned his attention to the
formalization of arithmetic, and the following year published a paper that
amazed and horrified the mathematical community. He demonstrated that any
consistent formal system that is powerful enough to do arithmetic must contain
undecidable statements - that is, statements whose truth or falsity cannot be
proved in the system - the First Incompleteness Theorem. To make matters worse,
he went on to show that the consistency of arithmetic itself must always be one
of these undecidable statements - the Second Incompleteness Theorem. (Note that
the system required for formalizing arithmetic is fairly weak, because
arithmetic is quite simple - so there is absolutely no hope for any consistent
formalization of more complex systems, such as ethics, for example!)
Let us consider just what Gödel's discovery means. A formal system is supposed
to be self-contained - in the case of an axiomatic formal system like Peano
arithmetic, which is the system that Gödel was investigating, all the theorems
that we might expect to be part of the system should be capable of being derived
from the axioms using the system's rules of inference. The derivation might be
very difficult, but theoretically it should be possible. One of the theorems
that formalist mathematicians had expected to be derivable in Peano arithmetic
was that the system was itself consistent. Gödel showed that the consistency of
Peano arithmetic (or axiomatic number theory, as it is also known) could only be
proved from outside the formal system. In other words, if we want a system of
arithmetic that can be formalized, we can never prove that, when working in that
system, we are not liable to contradict ourselves. This result dealt a
devastating blow to Hilbert's programme, and proved that all of mathematics
could not be derived from the principles of logic.
Gödel's proof is deep and very subtle, but a brief description can be given
here. His method of proof is to make theorems in the formal system of Peano
arithmetic say something about theorems of the system - in particular, to make a
theorem in the system say something about itself. This use of self-reference
seems as if it might lead to paradox, as in the case of Russell's set-theoretic
paradox or the liar paradox. However, Gödel avoids paradox by distinguishing
clearly between metamathematical theorems about the system, and theorems in the
system.
The symbols of the formal system of arithmetic are represented by numerals and
symbols such as "=" (equals) and """ (for all), and the
rules and theorems for manipulating the symbols are rules for manipulating
numerals. But a rule for manipulating numerals can be interpreted as a rule of
arithmetic - in the same way that, in the decimal system, shifting a numeral one
column to the left and suffixing it with a zero can be interpreted as
multiplying the number that the numeral represents by 10. Theorems derived in
the formal system thus have a double meaning, and by distinguishing clearly
between the two interpretations of the theorem - the symbolic and the arithmetic
- paradoxes of self-reference are avoided..
Gödel began with Peano's axioms of arithmetic, together with a basic system of
logic that was powerful enough to carry out proofs in Peano arithmetic. He
invented a code, called Gödel numbering or Gödelization, by means of which any
theorem of Peano arithmetic could be represented by a unique natural number. In
this way, a theorem that ordinarily makes a statement about numbers (and not
another theorem) could be interpreted as saying something about another theorem
(via its Gödel number). Gödel then proceeded by making a theorem of Peano
arithmetic say something about itself - specifically, that it could not be
proved within the constraints (the axioms and rules of inference) of the formal
system. In other words, this theorem was undecidable in the formal system.
Gödel also showed that no matter how many further axioms are added to the
system, it remains incomplete - there will always be undecidable propositions,
which can be proved, if at all, only by appealing to metamathematical arguments
outside the system. This result is often interpreted as proving that artificial
intelligence is an impossible dream, because there is a limit to how many times
computers can leap outside of a system to consider a question from a higher,
"meta-" viewpoint.