points. Prove that
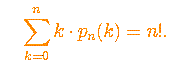 (Remark: A permutation f of a set S is a one-to-one mapping of S onto itself. An element
i in S is called a fixed point of the permutation f if f(i) = i.)
(Remark: A permutation f of a set S is a one-to-one mapping of S onto itself. An element
i in S is called a fixed point of the permutation f if f(i) = i.)| home | stands | games | about | mpjournal | back | links |
1. Let pn(k) be the number of permutations of the set {1, . . . , n}, n
³ 1, which have exactly k fixed
points. Prove that 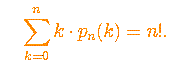 (Remark: A permutation f of a set S is a one-to-one mapping of S onto itself. An element
i in S is called a fixed point of the permutation f if f(i) = i.)
(Remark: A permutation f of a set S is a one-to-one mapping of S onto itself. An element
i in S is called a fixed point of the permutation f if f(i) = i.)
2. In an acute-angled triangle ABC the interior bisector of the angle A intersectsBC at L and intersects the circumcircle of ABC again at N. From point L perpendiculars are drawn to AB and AC, the feet of these perpendiculars being K and M respectively. Prove that the quadrilateral AKNM and the triangle ABC have equal areas.
3. Let x1, x2, . . . , xn be real numbers satisfying x12+x22+· · ·+xn2 = 1. Prove that for every integer k ³ 2 there are integers a1, a2, . . . , an, not all 0, such that |ai|£ k - 1 for all i and
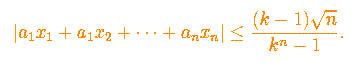
4. Prove that there is no function f from the set of non-negative integers
into itself such that
f(f(n)) = n + 1987 for every n.
5. Let n be an integer greater than or equal to 3. Prove that there is a set of n points in the plane such that the distance between any two points is irrational and each set of three points determines a non-degenerate triangle with rational area.
6. Let n be an integer greater than or equal to 2. Prove that if k2 +k +n is prime for all integers k such that 0 £ k £ Ön/3, then k2 + k + n is prime for all integers k such that 0 £ k £ n - 2.