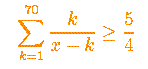29^th International Mathematical Olympiad
Canberra, Australia
Day I

1. Consider two coplanar circles of radii R and r (R > r) with the same center. Let P be a fixed point on the smaller circle and B a variable point on the larger circle. The line BP meets the larger circle again at C. The perpendicular l to BP at P meets the smaller circle again at A. (If l is tangent to the circle at P then A = P.)
(i) Find the set of values of BC² + CA² + AB².
(ii) Find the locus of the midpoint of BC.

2. Let n be a positive integer and let A₁, A₂, . . . , A_2n+1 be subsets of a set B. Suppose that
(a) Each A_i has exactly 2n elements,
(b) Each A_i \ A_j (1 £ i < j £ 2n + 1) contains exactly one element, and
(c) Every element of B belongs to at least two of the A_i.
For which values of n can one assign to every element of B one of the numbers 0 and 1 in such a way that A_i has 0 assigned to exactly n of its elements?

3. A function f is defined on the positive integers by f(1) = 1, f(3) = 3, f(2n) = f(n),
f(4n + 1) = 2f(2n + 1) − f(n), f(4n + 3) = 3f(2n + 1) − 2f(n), for all positive integers n. Determine the number of positive integers n, less than or equal to 1988, for which f(n) = n.

Day II

4. Show that set of real numbers x which satisfy the inequality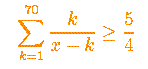 is a union of disjoint intervals, the sum of whose lengths is 1988.

5. ABC is a triangle right-angled at A, and D is the foot of the altitude from A.The straight line joining the incenters of the triangles ABD, ACD intersects the sides AB, AC at the points K, L respectively. S and T denote the areas of the triangles ABC and AKL respectively. Show that S ³ 2T.

6. Let a and b be positive integers such that ab + 1 divides a² + b². Show that (a²+b²)/(ab+1) is the square of an integer.