Sine, Cosine, and Tangent
Cosine and Sine Rules
                The Cosine Rule    The Sine Rule    Finding the Length of a Side    Finding the Size of an Angle    The Ambiguous Case
Angle Reference Table

Sine, Cosine, and Tangent

In a right-angled triangle, the size of any angle is related to the ratio of the lengths of any two sides by the trigonometric functions. The basic functions are sine, cosine, and tangent. These functions are based on the similarity of triangles that have a right angle and one other angle in common. Imagine an angle A formed by the intersection of lines AB and AC (see diagrams). A third line drawn perpendicularly up from AC gives a right-angled triangle. The sides of such a triangle will always be in the same ratio to one another, no matter where the third line intersects AC.
Sine
The sine of angle A is the ratio of the lengths BC to AB.
Cosine
The cosine of angle A is the ratio of the lengths AC to AB.
Tangent
The tangent of angle A is the ratio of the lengths BC to AC.

Cosine and Sine Rules

Relationships between the lengths of the sides and the sizes of the angles of any triangle are given by the cosine and sine rules. Provided we have enough information already, we can use the cosine and sine rules to find the length of a side, or the size of an angle. We usually use these methods only for triangles that do not have a right angle because easier methods for finding the dimensions of right-angled triangles exist.

The Cosine Rule

The cosine rule states that, for the triangle ABC in Diagram 1,
                a² = b² + c² - 2bccosA

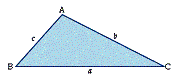
Diagram 1

Go to top

We can use the cosine rule to calculate the length of the third side of a triangle if we know the lengths of the other two sides and the size of the angle between them (the included angle). For example, suppose we want to find the length of side a in the triangle in Diagram 2.

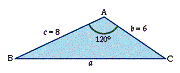
Diagram 2

We know that length b = 6, length c = 8, and angle A = 120°. Therefore, we can use the cosine rule, as follows:
                a² = b² + c² - 2bccosA
                    = 6² + 8² - 2 × 6 × 8 × cos120°
                    = 36 + 64 - 96 × -0.5
                    = 148
Therefore,
                a = Ö148
                   = 12.166 (to 3 decimal places)
We can also use the cosine rule to find the size of any angle of a triangle if we know the lengths of all three sides. For example, suppose we want to find the size of angle A in the triangle in Diagram 3.

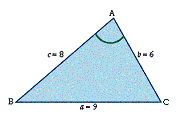
Diagram 3

Go to top

We know that length a = 9, length b = 6, and length c = 8. Therefore, we can use the cosine rule to find angle A, as follows:
                a² = b² + c² - 2bccosA
Rearranging this formula gives us
                cosA=(b²+c² - a²) / 2bc
So,
                cosA=(6²+8² - 9²) / 2x6x8
                        =(36+64 - 81) / 96
                        =19/96 = 0.19792...
Therefore,
                A = cos^-10.19792 = 78.585° (to 3 decimal places)

The Sine Rule

The sine rule states that, for the triangle ABC shown in Diagram 4,

where R is the radius of the circumcircle (the circle that passes through A, B, and C, and is said to circumscribe the triangle ABC).

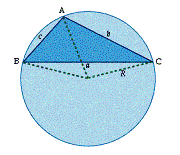
Diagram 4

Go to top

The sine rule can be used to obtain information about a triangle if we know the length of one side and the sizes of two angles. To use the sine rule in this way, we need to know the size of the angle that is opposite the side whose length we know; thus in the triangle in Diagram 5 we need to know the size of angle A since it is opposite the side whose length is known, a.

Diagram 5

However, if we do not have the size of this angle, we can easily calculate it since we know the sizes of the other two angles. The sum of the interior angles of a triangle is always 180°, so the size of angle A in Diagram 5 is given by
                180° - (B + C) = 180° - (40° + 20°)
                                       = 180° - 60° = 120°

Finding the Length of a Side

Suppose we want to find the length of side b in the triangle in Diagram 5. We know that the length of side a = 12, that angle A = 120°, and angle B = 40° and, therefore, we can use the sine rule, as follows:

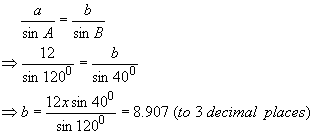
We could find the length of side c in a similar way.

Go to top

Finding the Size of an Angle

The sine rule can also be used to obtain information about a triangle if we know the lengths of two sides and the size of a nonincluded angle (that is, one of the angles that is not between the two sides whose lengths we know). If we know the lengths of two sides and the size of the included angle, we would use the cosine rule, as explained earlier.
Suppose we want to find the size of angle C in the triangle in Diagram 6.

Diagram 6

We know that the length of side a = 10, and of side c = 4, and that angle A = 130°, and so we can use the sine rule, as follows:

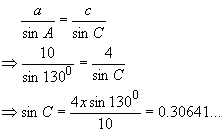
Therefore,
                C = sin^-10.30641 = 17.843° (to 3 decimal places)
We could find the size of the third angle, B, very easily by subtracting the sum of angles A and C from 180°, as we did earlier.

Go to top

The Ambiguous Case

Suppose we have the two triangles in Diagram 7.

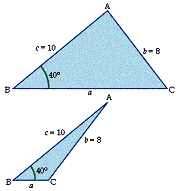
Diagram 7

In both triangles the angle B = 40°, the length of side b = 8, and the length of side c = 10. Suppose we want to find the size of angle C. Using the sine rule gives us

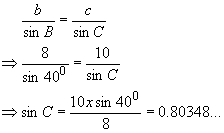
Therefore,
                C = sin^-10.80348 = 53.464° (to 3 decimal places)
This gives the size of angle C for the left-hand triangle, but angle C in the right-hand triangle is clearly greater than 90°. This is because there is also an angle between 90° and 180° for which sinC = 0.80348…. We can find this angle by taking the acute angle (53.464°) away from 180°. Thus the size of angle C in the right-hand triangle is given by
                180° - 53.4641° = 126.536° (to 3 decimal places)
This is called the ambiguous case since it is possible to draw two different triangles that both satisfy the original information.

Go to top

Angle Reference Table

This table gives the sines, cosines, and tangents of some commonly encountered angles.