pick's theorem

An ancient are calculation method

Many years ago people didn’t know about the world’s mysteries. They were interested in finding out and resolving them. Many scientists tried their best in different branches of science. Such as mathematics, geometry, physics, biology, geography, astronomy, chemistry, etc. So that they found many methods of finding the solutions to different kinds of problems.

4000-5000 years ago the greatest scientists in Egypt found the calculation to calculating areas of triangles, squares, rectangles, trapezoids. This calculation is very easy, because all sides are straight.

One of the interesting method of finding the area of any shape is calculated with a help of nails. Even you can find the area of complex figures using nails. Of course, there’re many different and interesting methods of resolving the area, but this crucial method is used by many people and the most important advantage of this method is that you can use it at home or where ever you want.

Aim

To find the area of complex figures.

Materials

First of all you need some nails, a board and colorful ribbons, hammer.

Method

Before you start to measure or calculate the areas of any shape, you should prepare the board. At first, take the board and measure it. Then draw some points on it, so the differences between them must be equal. After that take nails and drive them in the board, so your board is ready to serve you. Afterwards, take colorful ribbons and make different shapes by tying them on the nails. Now you’re ready to calculate the area of that shape. There is a little trick here. Remember the following:

Area = touching nails/2+(nails that are inside the shape, but not touching )-1
<go to top>

Conclusion

By this method you’re able to find the area of any complex shape.

<go to top>

Advanced...

Theorem

Let P be a lattice polygon. Assume there are I(P) lattice points in the interior of P, and B(P) lattice points on its boundary. Let A(P) denote the area of A. Then

Proof

For every lattice point p in the interior or boundary of P, let a_p denote the angle of visibility of P from p. For points in the interior of P, a_p = 2p. For points on the boundary other than vertices,      a_p = p . For a vertex p, a_p is just the internal angle of the polygon at that vertex. Let w_p = a_p/2p, and introduce W(P) = Sw_p, where the sum is taken over all lattice points either inside or on the boundary of P. Then
 

(1)	W(P) = A(P)

The proof of (1) proceeds in three steps. Firstly, note that function W is additive. Combining two polygons that share a piece of boundary into one either replaces two boundary points with one interior point or, when the point remains a vertex, adds up the two internal angles at that vertex, one from each polygon.
<go to top>

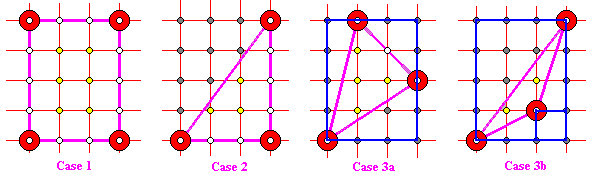
Secondly, verify (1) for simple shapes: lattice rectangle (Case 1) with sides parallel to the grid lines, half lattice rectangle (Case 2), and arbitrary lattice triangle where we have to consider a couple of cases (Cases 3a-b.) Embed the triangle into the smallest possible rectangle from Case 1. Such a rectangle will naturally appear as a union of the given triangle and pieces from the two previous cases. Apply additivity.

Thirdly, show that every simple lattice polygon may be dissected into a union of lattice triangle (e.g., by its diagonals.)

Acquipped with (1), we have only to compute W(P). Let P has n vertices and define b = B(P) - n. The sum of internal angles of P is (n - 2)*p. At all other boundary points p (whose number is b),     a_p = p. Therefore, Sw_p, where the sum is taken only over boundary points is (n - 2)/2 + b/2 = (n + b)/2 - 1 = B(P)/2 - 1. Adding the sum Sw_p over the internal points which is simply I(P) completes the expression for W(A):

This combined with (1) proves the theorem.
<go to top>

An application of Pick's Theorem in forestry

"Some years ago, The Northwest Mathematics Conference was held in Eugene, Oregon. To add a bit of local flavor, a forester was included on the program, and those who attended his session were introduced to a variety of nice examples which illustrate the important role that mathematics plays in the forest industry. On of his problems was concerned with the calculation of the area inside a polygonal area drawn to scale from field data obtained for a stand of timber by a timber cruiser. The standard method is to overlay a scale drawing with a transparency on which a square dot pattern is printed. Except for a factor dependent on the relative sizes of the drawing and the square grid, the area inside the polygon is computed by counting all of the dots fully inside the polygon, and then adding half of the number of dots which fall on the bounding edges of the polygon."