match1

You can do more with matches than just strike them. You can play lots of fun games with Matches. Some people construct the most beautiful objects by gluing thousands of matches together.

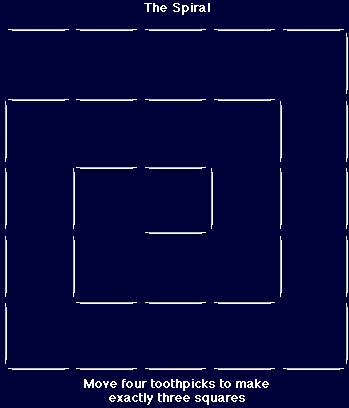
There are also match construction puzzles which do not use glue. These puzzles are often surprisingly difficult, as you will see if you try the two puzzles illustrated here.

For the above puzzle you will need 114 matches and for the bridge opposite you will need 18 long matches. Lots of patience and a steady hand are also essential.

Further, there are the well-known trick match puzzles, in which matches have to be repositioned and/or removed.

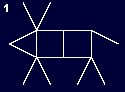	Figure 1: Opposite you see a match puzzle. With a little imagination you can recognize Louis, a French deer. Louis is looking to the left, but Louis is very inquisitive and would also like to know what's happening on the right. By repositioning two matches, can you let Louis look to the right?
	Figure 2:By repositioning 2 matches can you change this Star of David so that it consists of 6 triangles only?
	Figure 3: Reposition 4 matches to form 5 triangles.
	Figure 4:Two problems: a) remove 5 matches so that you are left with 5 equal triangles. b) reposition 6 matches so that you can make 6 equal lozenges in a symmetrical star pattern.
	Figure 5:Remove 3 matches so that you are left with 3 triangles.
	Figure 6:Opposite you see 7 equal triangles and one larger (8th) triangle. Reposition 6 matches to form 6 equal lozenges.
	Figure 7:Try to make the fish swim to the opposite direction by repositioning 3 matches.

	Figure 1:Remove 2 of the nine matches and reposition the seven left matches so that you're still left with a perfect cube.
	Figure 2:Replace 1 match so that you're left with a square.
	Figure 3:Reposition 4 matches so that you're left with 2 squares and four triangles.
	Figure 4:Use these six matches to form four equilateral triangles.
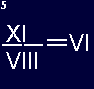	Figure 5:By repositioning just 1 match, you can make this equation correct.
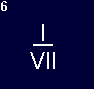	Figure 6:Shift one of the six matches opposite without touching the others so that the new arrangement shall represent an arithmetical fraction equal to 1.
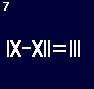	Figure 7:By repositioning just 1 match, you can make this equation correct.

Matches, obviously, and some common sense. Matches are easy to come by, but as for common sense... Match puzzles are often more difficult than they look at first sight. They are certainly not inferior to impressive 3D construction puzzles. Give it a try.

matches puzzles