| home | games | about | mpjournal | school | links |
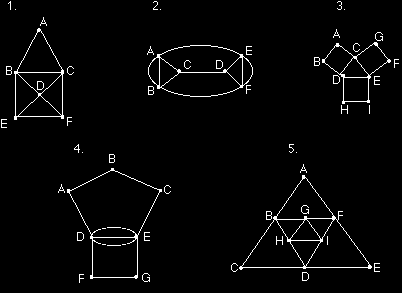
Can you trace the pictures without retracing any lines and without lifting your pencil?
Yes! All five figures can be traced.
Count then number of edges that come from each point. Find the all points with an odd number of edges, these must be your starting and ending points. If you have more than two you would not be able to trace the drawing.
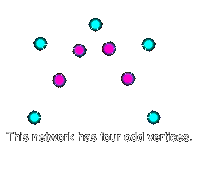
If you have no points with an odd number of edges (numbers 3 and 5) then you can start your tracing at any one of the points and you will be able to trace the figure ending it at the same point.
Topology is one of the newest branches of mathematics. A simple way to describe topology
is as a 'rubber sheet geometry' - topologists study those properties of shapes
that remain the same when the shapes are stretched or compressed. The 'Euler number' of a
'network' like the ones presented later in this discussion is an example of a
property that does not change when the network is stretched or compressed.
The foundations of topology are often not part of high school math curricula,
and thus for many it sounds strange and intimidating. However, there are some
readily graspable ideas at the base of topology that are interesting, fun, and
highly applicable to all sorts of situations. One of these areas is the topology
of networks, first developed by Leonard Euler in 1735. His work in this field was inspired by the following problem:
<go to top>
In Konigsberg, Germany, a river ran through the city such that in its center was an island, and after passing the island, the river broke into two parts. Seven bridges were built so that the people of the city could get from one part to another. A crude map of the center of Konigsberg might look like this:
The people wondered whether or not one could walk around the city in a way that would involve crossing each bridge exactly once.
Try it. Sketch the above map of the city on a sheet of paper and try to
'plan your journey' with a pencil in such a way that you trace over each
bridge once and only once and you complete the 'plan' with one continuous
pencil stroke.
<go to top>
Suppose they had decided to build one fewer bridge in Konigsberg, so that the map looked like this:
Now try to solve the problem.
Does it matter which bridge you take away? What if you add bridges? Come up
with some maps on your own, and try to 'plan your journey' for each one.
<go to top>
Euler realized that all problems of this form could be represented by replacing areas of land by points (he called them vertices), and the bridges to and from them by arcs. For Konigsberg, let us represent land with red dots and bridges with black curves:
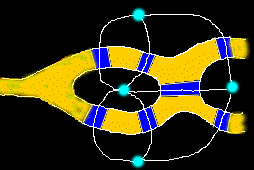
Thus, in its stripped down version, the seven bridges problem looks like this:
The problem now becomes one of drawing this picture without retracing any line and without picking your pencil up off the paper. Consider this: all four of the vertices in the above picture have an odd number of arcs connected to them. Take one of these vertices, say one of the ones with three arcs connected to it. Say you're going along, trying to trace the above figure out without picking up your pencil. The first time you get to this vertex, you can leave by another arc. But the next time you arrive, you can't. So you'd better be through drawing the figure when you get there! Alternatively, you could start at that vertex, and then arrive and leave later. But then you can't come back. Thus every vertex with an odd number of arcs attached to it has to be either the beginning or the end of your pencil-path. So you can only have up to two 'odd' vertices! Thus it is impossible to draw the above picture in one pencil stroke without retracing.
More puzzles to try yourselves...
