D
=
7 1/5°
C
360°
An Early Measurement of the Circumference of the Earth
In about 200 BC, an astronomer and mathematician named Eratosthenes (276-194 BC) wanted to derive a method to find the circumference of the Earth.
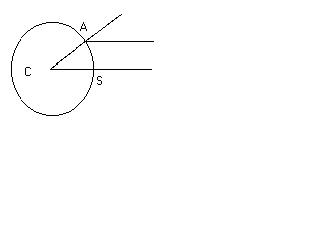
On the day of the summer solstice (June 21st, the longest day of the year), Eratosthenes knew the sun was directly overhead at Syene, a place on the Tropic of Cancer. He knew that this was true because the sun shone straight down a well there, only on that day of the year. At the same time in Alexandria, which he knew was approximately 5000 stades north of Syene, the sun produced a small shadow to 7 1/5° from the zenith.
Since the rays of light were parallel, the angle Ð SCA is the same as at Alexandria. He constructed the following ratio:
|
D |
= |
7 1/5° |
 |
|
C |
360° |
where D represents the distance between Alexandria and Syene,
where C is the circumference of the Earth.
Eratosthenes solved for C, and discovered the earth had a circumference of
|
C = |
(5000)(360° ) |
|
7 1/5° |
|
|
= |
25 000 stades |
It turns out that 1 stade = 1/6 km. So, C @ 42 000 km. Today, from scientific equipment we know the actual circumference of the earth is about 40 000 km. Eratosthenes is also credited with many other mathematical and astronomical discoveries, including a method for finding all the prime numbers below any integer value.
|
D |
= |
7 1/5° |
|
C |
360° |