Problems On Pythagorean Theorem

Problem #1 -- Alison, Jennifer and Samantha

While visiting Toronto, Marissa saw many tall buildings. One night Marissa had a dream about a building 250 m tall with huge ladder leaning up against it. The ladder was 160 m long. It was propped up against the building so that the bottom was 120 m away from the side of the building. Marissa wondered how far up the building the ladder reached. Can you tell her?
Marissa can use the Pythagorean Theorem. Let the length of the unknown side be x. Then we have: 1602 = 1202 + x2 1602 - 1202 = x2 25600 - 14400 = x2 11200 = x2 ± 105.8 = x So, the ladder was stretching about 106 m up the building.

Problem #2 -- Brian, Amy and Sean

Elliot was on a hiking trip in the Rockies. As the group came to the edge of one of the cliffs, Elliot saw that the bridge they were about to cross had support beams in the shape of a right angled trianlge. Elliot saw that the sign by the bridge said that one beam was 500 metres long and the other was 600 metres long. Help Elliot to figure out the length of the bridge across the valley.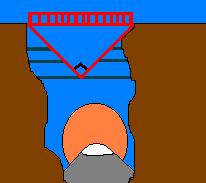
Let d represent the length of the bridge. By the Pythagorean theorem, we have: d2 = 5002 + 6002 d2 = 250000 + 360000 d2 = 610000 d = ± 781.025 d = 781 m So, the bridge was about 781 m across the valley.

Problem #3 -- Chris, Jenni, and Kyle

Pythagoras was concerned with all sorts of interesting problems, including one involving squares. The problem involved finding the length of a side of a square which is constructed from the diagonal of a sqaure which is half the length of a square below it. If the bottom square has sides of length 4 cm and the middle square has sides with half that length, what is the length of the sides of the square on the diagonal?
Let l represent the length of the unknown side on the purple square. Since l is the diagonal of the middle square, it is actually the hypotenuse of a right angled triangle (the blue triangle). Then by the Pythagorean theorem, we have: l2 = 22 + 22 l2 = 4 + 4 l2 = 8 l = ± 2.828 l = 2.8 cm The length of the side of the purple square is 2.8 cm.

Problem #4 -- Eric, LaToya, and Lynn

Jennifer hates taking the longest route anywhere. She likes to leave at the last minute and get there right on time. Sometimes when Jennifer leaves late, she decideds to jaywalk across Division and Concession streets. (It is 25 footsteps across Division and then 35 across Concession streets.) Jennifer knows she takes less footsteps by going on a diagonal than by crossing both streets. Explain, with mathematics, why this is true.
Jennifer knows this is the shortest way because she was in Miss Lang's grade nine math class for the lesson on the Pythagorean theorem. If Jennifer were to cross properly at the two cross walks, she would use a total of 25 + 35 = 60 footsteps. However, by going on the diagonal, she can use the Pythagorean theorem to show that she takes less footsteps. Let f represent the number of footsteps she takes when she jaywalks. Then: f2 = 252 + 252 f2 = 625 + 1225 f2 = 1850 f = ± 43.01 f = 43 footsteps When Jennifer crosses the street on the diagonal, she only takes about 43 or 44 footsteps. So she saves about 17 or 18 steps and she can get farther down the street!

Problem #5 -- Steven, Matthew, and Andy

A curious student wondered if she could figure out the length of the sides of a square by only knowing the length of the diagonal of the square. If the length of the diagonal is 27 units, can she do this?
Yes, she can. Since it is a square, then the lengths of the sides are the same. Using the Pythagorean theorem, she can find the length of the sides. Let the sides be given by s. Then she finds: 272 = s2 + s2 272 = 2s2 729 = 2s2 364.5 = s2 ± 19.092 = s s = 19.1 units The length of each side of the square is about 19.1 units long.

Problem #6 -- Zoe, Darcy, and Taylor

A baseball diamond is a square 27.5 m on each side. James catches for the school team, the Eagles. He often throws the ball from home plate to second base to stop an opponent from stealing a base. How far did James throw the ball?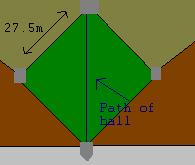
Let the distance the ball travelled be b. We can use the Pythagorean theorem because the bases make right angles: b2 = 27.52 + 27.52 b2 = 2*(756.25) b2 = 1512.5 b = ± 38.89 b = 38.9 m James threw the ball 38.9 m to the second baseman.

Problem #7 -- Terry, Pat and Chris L

If the two diagonals of a field are the same length, the field has square corners. How long is each diagonal in a field measuring 80 m by 70 m with square corners?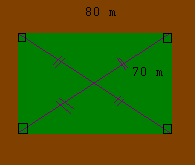
Let the diagonal be given by d. Using the Pythagorean theorem, we find that: d2 = 802 + 702 d2 = 6400 + 4900 d2 = 11300 d = ± 106.31 d = 106.3 m The length of each of the diagonals is 106.3 m.

Problem #8 -- Rob, Wes, and Greg

Jenna was walking home one day staring at her roof top as she approached her house. She was thinking about attics in houses and how she didn't know if her house had a useable one. Her Dad told her that the house was 1200 cm wide and the rafter was 671 cm long. Jenna decided to find out how high the peak in the attic was, and if it was high enough for her to play in. (She is 150 cm tall.) Can you help her?
First we have to find the height of the peak in the attic. Let the peak height be given by p. Because it's a right angle, then the Pythagorean Theorem gives: 6712 = p2 + 6002 6712 - 600 2 = p2 450241 - 360000 = p2 90241 = p2 ± 300.401 = p p = 300.4 cm Since the height of the peak is 300.4 cm, and Jenna is only 150 cm tall, then it's almost twice her height, so she can stand in it and play if she wants.

Problem #9 -- Melissa, Tara and Nancy

A ramp is to be built from the top level of one parking garage to another. The smaller building is 15 m tall, and the larger is 19 m tall. There is a distance of 12 m between them. Calculate the length of the ramp to the nearest tenth of a metre.
Let the length of the ramp be r. Since we can make a right angle triangle if we draw a line from the edge of the smaller building to the taller building, we can figure out the lengths we need. The length of the bottom of the triange is 12 m, which is the distance between the two buildings. The height of the triange is the difference between the small building's height and the taller one. So this is: 19 m - 15 m = 4 m So then we can use the Pythagorean theorem to find the length of the ramp: r2 = 122 + 42 r2 = 144 + 16 r2 = 160 r = ± 12.649 r = 12.6 m The length of the ramp is 12.6 m long.

Problem #10 -- Vic, Sasa, and Rich

Anne and Chan are on a hike. They come to a field that is rectangular and measures 3.0 km by 1.6 km. Anne decides to take a short cut and walk diagonally across the field. Chan walks around two sides of the field. Who walks farther and by how much?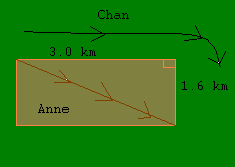
Since the field is rectangular, then the diagonal makes a right angle triangle. By the Pythagorean theorem, we know that the shortest distance is along the diagonal. So then we know that Chan walked the farthest. To find who walked the farthest, we find the length that Anne walked. Using the Pythagorean theorem, we let the distance Anne walked be a: a2 = 32 + (1.6)2 a2 = 9 + 2.56 a2 = 11.56 a = ± 3.4 a = 3.4 km So Anne walks 3.4 km. Now, Chan walks all the way around, so then he walks a total of: 3.0 km + 1.6 km = 4.6 km So the difference in their distances is: 4.6 km - 3.4 km = 1.2 km So Chan walks the longest and walks 1.2 km more than Anne.

Problem #11 -- Emily, Liam, and Ayeka

Find the length, to one decimal place, of the unknown lengths in the diagram.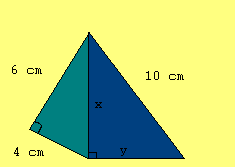
We need to find both lengths x and y. We can find x first by using the Pythagorean theorem on the smaller triangle. Then the length of x is given by: x2 = 62 + 42 x2 = 36 + 16 x2 = 52 x = ± 7.211 x = 7.21 cm Now that we know the length of side x, we can find length y. Using the same method we find the length of y to be: 102 = y2 + x2 100 = y2 + 52 100 - 52 = y2 48 = y2 ± 6.92 = y y = 6.9 cm So the lengths of the unknown sides are: x = 7.2 cm and y = 6.9 cm.

Last updated March 4 by Miss Lang

Home

Use Internet In The Classroom