1]
     Use mathematical induction to prove for all positive integers n the following proposition.

     


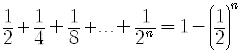
SOLUTION

Step 1.
Check the proposition for k=1. That is, for the series with one term.

        is a true statement.

Let's do one more check, for k = 2. That is, for the series with two terms.

        Is this statement true?

The left side is
     .

The right side is

     

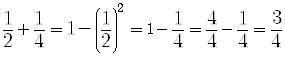
So the formula is true for these initial values.
The first step of the mathematical induction process is verified.

Step 2.
If the proposition is true for n = k, then we must prove that it is true for n = k+1.
In other words, we must prove that if the proposition is true for one value of n,
then it is true for the next succeeding value of n.
This induction establishes that the proposition is true for all values of n.

Assume that

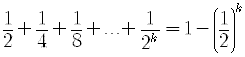        is true.

For n = k+1, the next term in the series will be

     .

Add this term to both sides of the above equation.
We get

      .

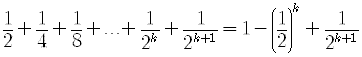Work out the right side to see if it can be written in the form required by the proposition.

          

     

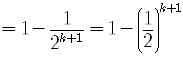     ,    which is the required form.


The mathematical induction proof is then complete.




2]
     The sequence is arithmetic. Find the indicated quantity.

     


SOLUTION
The formula for the nth term of an arithmetic sequence is

     .

In our problem the common difference is

        and   .

     




3]
     The sequence is geometric. Find the indicated quantity.

     


SOLUTION
The formula for the sum of the first n terms of a geometric series is

     .

     




4]
     Find the sum.

     


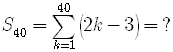
NOTE: The solution of this problem will use an appropriate formula
that we have studied in this section.
Finding the sum of the series by using your calculator to add up
all the terms of the series is NOT acceptable as the solution to the problem.

SOLUTION
To determine whether the series is arithmetic or geometric,
it is a good idea to write out the first few terms of the expansion.

     

     

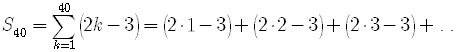
This is an arithmetic series with

        the first term of the series

        the common difference of the series

        the number of terms of the series

A formula for the sum of the first n terms of an arithmetic series is

     .


     



5]
     Find the sum of the infinite series.

     


SOLUTION
The series is geometric with

        the first term of the series

        the common ratio of the series


The formula for the sum of an infinite geometric series is

     .

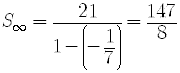        is the answer.





6]
     Represent the infinitely repeating decimal as the quotient of two integers.

     


SOLUTION
We can write

     

The decimal part

     

     


     

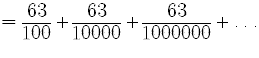
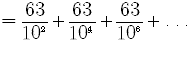
is a an infinite geometric series with

        the first term of the series

        the common ratio of the infinite series

The formula for the sum of an infinite geometric series is

     .

So the answer to our problem is

     






                                                                           top




© edmond 2003