Write in simplified form
.SOLUTION
The easiest way to do this problem is to rewrite the radical, using rational exponent notation.
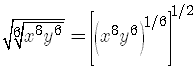
Now use exponent rules. It is a good idea to follow the rules for the order of operations:
1] Do what's inside the parenthesis first.
If there are parentheses within parentheses, do what's inside the innermost parentheses first,
then work yourself out to the outermost parentheses.
2] Secondly, work out the powers.
3] Thirdly, do the multiplications and divisions, going from the left side to the right side of the
expression.
4] Fourth, and finally, do the additions and subtractions, going from the left side to the right side
of the expression.
So
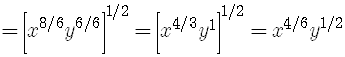
The problem was given in terms of radicals, so let's write the final answer as a radical expression.
Since the denominator of the rational exponent gives us the root, to write the above expression
as a single radical we only need to express the rational exponents in terms of the lowest common
denominator (LCD).
Here the LCD is
. 
2]
Solve the rational equation
.SOLUTION
The main reason why students have trouble solving rational equations
is they do not use the method that is shown to them.
The method is to multiply the equation by the LCD of all the fractions that are in the equation.
The result of this multiplication is that you get an equation with no fractions at all!
Remember, the LCD is written as an appropriate product of all the factors that appear
in all the denominators in the equation.
Here,
can not be factored, so the 
.Multiply the fractional equation by the LCD.
That means, multiply the left side and the right of the equation by the LCD.
You have to do the same thing to both sides of the equation;
otherwise, you wouldn't have an equation anymore.
Remember, in algebra you multiply by using the distributive law
.left side of the equation
right side of the equation
Now cancel any common factors that appear.
left side right side
Work out the product using the distributive law.
We are not finished yet!
In rational equations, we must always check the numbers in the original equation.
If we wind up dividing by zero in the original equation, for example, if got b=5 or b=5,
then the numbers we got do not work in the original equation.
So the answer to the problem of solving the equation is NONE.
The equation has no solution.
However, in our case, we do not divide by zero in the original equation, so
IS the solution.3]
Solve the system of equations by the method of substitution,
.SOLUTION
The idea of the method of substitution is to pick one of the two equation,
it really doesn't matter which one.
But, of course, we want to pick the one that will be easiest to work with.
In this problem , there are factions.
If you don't like fraction, get rid of them
by multiplying the first equation by 8, the LCD of 2 and 8;
and multiplying the second equation by 10, the LCD of 5 and 10.
or
Now let's begin the method of substitution.
Pick the first equation and solve it for
.
Substitute this expression for
into
the second equation.
To determine the corresponding value of
,
substitute
into .
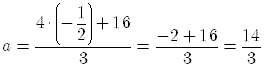
So the solution of the system of equations is given by the point of intersection
.
top
© edmond 2003