Algebra B Practice 3 Module 2 Problems relating to sec 2.3, 2.4, 2.5
	1]      Solve and graph the inequality       SOLUTION The goal is get the unknown quantity      alone. The final answer should look like      . We must determine what the numbers on either side of the    must be. Let's start the process of isolating the   . Subtract 7 from all three sides of the inequality             Now, get rid of the fraction by multiplying the inequality by 5             We are almost there! To get    alone, divide the inequality by   -2. But - remember! - when we multiply or divide an inequality by a negative number , the sense of the inequality reverses.         becomes   , so             or equivalently       In set-builder notation, this - the solution set of the inequality - is written as       and is read as "the set of all x such that -35 is less than or equal to x and x is less than or equal to -20". Always write the final answer in set-builder notation. The graph is       The solid dots indicate that the endpoints are included in the solution set. A hollow dot indicates that the point is not included in the solution set. Equivalent notation is to use a bracket   ( [ or ] )   to indicate the inclusion of the point or curl parenthesis   ( ( or ) )   to indicate the exclusion of a point. In this notation the above closed interval would be written as   [-35, -20] . 2]      For what real number(s)    does the expression       represent a real number? SOLUTION We can not take the square roots of negative numbers      (doing so would result in an imaginary number, not a        real number), so the radicand must always be positive or zero.       The goal always is to isolate the  , as in the previous problem.             Again, we must divide by a negative number so the sense of the inequality reverses.             In set-builder notation, 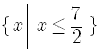     . 3]      Solve the inequality. Write answers using both inequality notation and interval notation.       SOLUTIOJ Re-write the inequality without the absolute value sign.                   To isolate the  , divide by  3, a positive number so the sense of the inequality does not reverse.             The final answer is 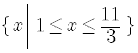     . In interval notation, this would be written as 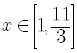     . A square bracket indicates the point is included in the set. A curved bracket, or parenthesis, indicate the point is not included the set. For example, the interval      would be written in inequality notation as      . 4]      Solve the inequality.       Write answers using both inequality notation and interval notation. SOLUTION Re-write the inequality without the absolute value sign.         or   Separately solve each of the inequalities. Let's start with the first inequality.             Now divide by a negative number so the sense of the inequality reverses.             This is the solution for the first inequality. Now let's do the second inequality.                   Divide both sides by a negative number so the sense of the inequality reverses.             So the solution set of the original absolute value inequality       consists of the set of numbers such that         or   In set-builder notation,      . In interval notation,         or   .         is the infinity symbol. 5]      Perform the indicated operation and write the final answer      in the standard form for complex numbers,   .       SOLUTION To get rid of the complex number in the denominator, multiply the numerator and the denominator by the complex conjugate of the denominator, viz., .       Remember that   .       The final answer in standard form is       .                                                                     top © edmond 2003