1]
Using the quadratic formula, solve
SOLUTION
Write the quadratic equation in standard form, that is, with zero alone on one side of the equation.
so that we can read off the values of the coefficients to use in the quadratic formula
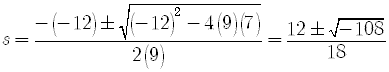
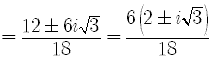
2]
Using a calculator, solve to two decimal places
SOLUTION
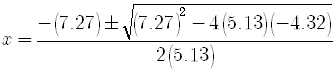
3]
Solve the radical equation
SOLUTION
The method is to isolate one of the radicals.
That is, have one of the radicals - it doesn't matter which one - alone on one side
of the equation and have everything else on the other side of the equation.
Let us isolate the first radical. That is, the first square root.
Now square both sides of the equation
in order to get rid of the square root on the left side of the equation.
Use the identity for the square of a sum
to work out the right side of the equation.
There is another radical remaining on the right side of the equation,
so we must repeat the process and isolate the radical.
Square the equation.
Use the identity for the square of a difference
to work out the left side of the equation.
Write the equation in standard quadratic form.
Factor the left side of the equation.
If the factoring appears too difficult, we can use the quadratic formula to solve the equation.
Now use the Zero Product Property:
If a product
then either
In other words, if a product is equal to zero,
then some of the factors involved in the product must be equal to zero.
So
But we aren't finished yet!
We must check whether the numbers work in the original equation - the radical equation -
that we wanted to solve
CHECK:
For
Is
For
Is
So
4]
Solve
SOLUTION
This is an example of an equation that is reducible to quadratic form
after an appropriate substitution.
Let
Solve it using the quadratic formula.
Here
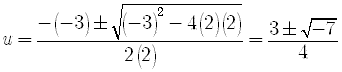
Remember that
so the above is
We want the values of
Remember the laws of exponents.
When we raise a power to a power, we multiply the exponents.
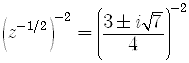
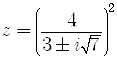
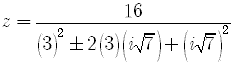
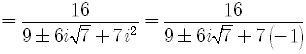
All answers involving complex numbers must be written in the standard form
Multiply the numerator and the denominator of the fraction
by the complex conjugate of the denominator, namely ,

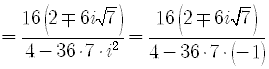

top
© edmond 2003