1]
Solve and graph. Express answer in both inequality and interval notation.
SOLUTION
Solve the equation
The only zero is
We must exclude the points where the denominator is equal to zero,
because we can not divide by zero.
The solutions of the equation
are
let's indicate the points corresponding to these numbers on the number line.
To facilitate talking about the fraction, let
Evaluate
If
Likewise, if it is negative at a single point, then it is negative at all the points in the subinterval.
The above graph is the result of such computations.
For example,
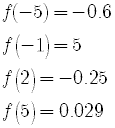
From the graph we can read the solution set for the problem.
We are looking for those intervals with the negative signs.
The solution set is
0 and -2 are excluded from the solution set because at those points
the denominator is zero and division by zero is inadmissible.
4 is included in the solution set because the inequality in the problem is
"
The rational function can be equal to zero.
2]
Find the center and the radius of the circle with the given equation.
Graph the equation.
SOLUTION
We need to put the equation in the standard form of the equation of a circle
in order to read the coordinates of the center
Completing the squares on the
So the center of the circle is at
3]
Write an equation for the line that contains the indicated point
and satisfies the indicated condition.
Write the answer in the standard form
(a)
SOLUTION
so the slope of the given line is 4
and the slope of any other line parallel to it is also 4.
We use the point-slope form of the equation of the straight line
to finish the problem.
Substitute the coordinates of the given point
(b)
SOLUTION
Writing the given line in the slope-intercept form
we see that the slope
So the slope of any other line perpendicular to the given line is
The given point is
As in the previous problem:
top
© edmond 2003