1]
     Find and simplify

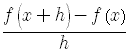     ,   given that  


SOLUTION

     

     


     

     

     

     
     


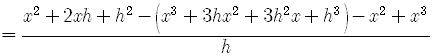
2]
     Graph, finding the domain, range, and any points of discontinuity.

     


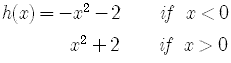
SOLUTION

The graph has a gap at x = 0.
It jumps from the lower branch to the upper branch,
so x = 0 is a point of discontinuity of the function.
The domain consists of all the real numbers except for x =0.
In set-builder notation

     .

In interval notation

     .

The range consists of all the real number greater than 2 or all the real numbers less than 2.
In interval notation

     .

Look at the graph.


          


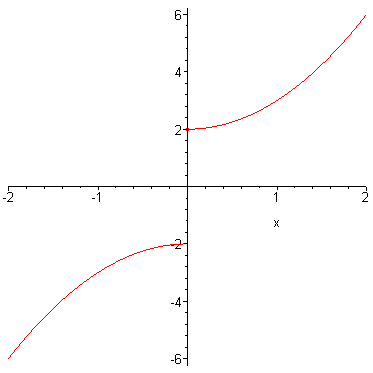
3]
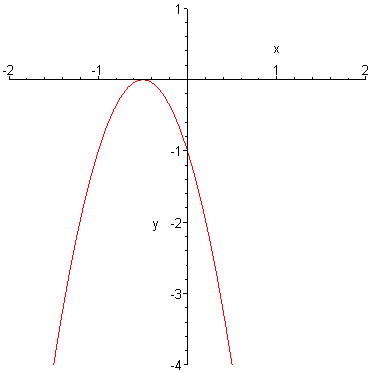
     Graph, finding the equation of the axis of symmetry, the coordinates of the vertex,
      maximum or minimum value of f(x), the range, intercepts, and intervals over which
      f is increasing, and intervals over which f is decreasing.

     

Note: The graph is called a parabola.


SOLUTION

Using the method of completing, we must put the equation in the standard form

     

in order to be able to read off the coordinates of the vertex

     

Complete the squares inside the parentheses.

     

     

     
The equation is now in standard form. The vertex is at   .

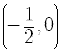The equation of the axis of symmetry is   .

The parabola opens downward so the vertex is the highest point on the parabola,
therefore corresponding to the maximum value of the function.
In other words , the maximum value of the function occurs at   .
The maximum value of the function itself  .

The range consists of all the real numbers less than or equal to 0.
In interval notation,
                                        .

To find the y-intercept, set x = 0 and solve the equation for y.
The function values f(x) are the y values.

     

The y-intercept is the point

      .

To find the x-intercept, set y = 0 and solve the equation for x.

     

Multiply the equation by -1 to make all the coefficients positive.

     

Factor the left side.

     
The solution is
           , a root of multiplicity 2.

The x-intercept is the point

      .

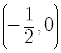At this point, the parabola is tangent to the x-axis.

        is increasing on     and decreasing on   .

Look at the graph of the function.


          






4]
     Find   and its domain, given

             and   .


SOLUTION

     


     


The point,   ,  at where the denominator is equal to zero
must be excluded from the domain of the function.
The domain of      is
                                                      .





                                                                    top



© edmond 2003