1]
The function is 1-1. Find
SOLUTION
The domain and the range of the function are
Set
To eliminate the cube-root, raise both sides of the equation to the third power.
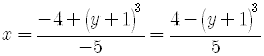
Now, following the process of finding
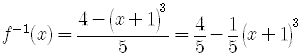
The domain and the range are
2]
Using synthetic division and the Remainder Theorem ,
find
SOLUTION
By synthetic division,
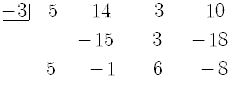
The third line gives the result of the synthetic division process.
According to the Remainder Theorem, the last number of the third line, the remainder, is the
value of the given polynomial evaluated at
3]
Find all the roots exactly (rational, irrational, and imaginary) of the polynomial equation
SOLUTION
By the rational Roots Theorem, the possible rational roots are
By synthetic division,
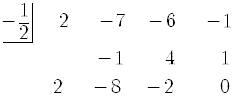
So
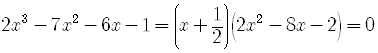
The second factor is quadratic and we know how to solve quadratic equations.
By the quadratic formula,
 .
.The roots of the third degree polynomial equation are
4]
Use synthetic division table and the
Location Theorem:
If
in
least
one  intercept between
intercept between  and
and  .
.
Locate each real zero of the polynomial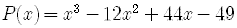
between successive integers
SOLUTION
The following table gives the results of the synthetic division for the integers 2, 3, 4, 5, 6, 7.
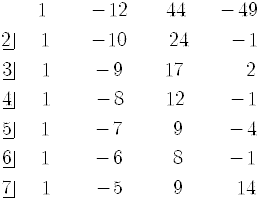
The last number in each line (after the first line)
is the value of the polynomial evaluated at the given point.
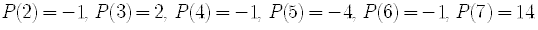
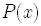 changes
sign in the intervals
changes
sign in the intervals 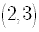 ,
,
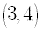 ,
and
,
and  .
.
We have located three real zeros as being within each of the above intervals.
Since the polynomial is of the third degree, it has only three zeros ,
so we have located all of them.
top
© edmond 2003
Locate each real zero of the polynomial
between successive integers
SOLUTION
The following table gives the results of the synthetic division for the integers 2, 3, 4, 5, 6, 7.
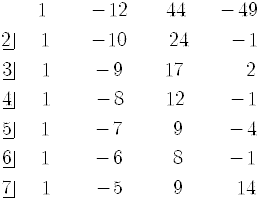
The last number in each line (after the first line)
is the value of the polynomial evaluated at the given point.
We have located three real zeros as being within each of the above intervals.
Since the polynomial is of the third degree, it has only three zeros ,
so we have located all of them.
top
© edmond 2003