1]
     Sketch the graph of the rational function.

     

SOLUTION


          




2]
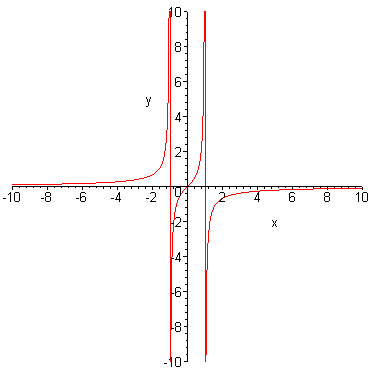
     Find all vertical, horizontal, and oblique asymptotes of the rational function.
      Do not graph.

     


SOLUTION
The vertical asymptote occurs where the denominator of the rational function vanishes.

     

        is the equation of the vertical asymptote.

To find the horizontal asymptote, divide the numerator and the denominator
of the rational function by the highest power of     occurring in the function, namely, .

           

As   ,   both    and the other fraction go to zero.
The numerator of the rational function remains constant,
while the denominator becomes smaller and smaller,
so the value of the rational function gets bigger and bigger beyond all bounds.
That is, the graph of the rational function keeps on rising up beyond the bound
of any horizontal line.
Conclusion:     has no horizontal asymptote.

To find the oblique asymptote, perform the algebraic long division indicated.


          

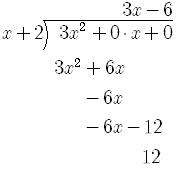
The remainder is 12.

So

     .

As   ,   the remainder term   .

So the rational function      behaves more and more like    
which is a linear function whose graph is a straight line.
Conclusion: 
                              has an oblique asymptote whose equation is

                                                                 


3]
     Solve the exponential equation

     

Note: The exponent attached to the 4 is 5x+1.


SOLUTION
The goal, if possible, is to rewrite the equation so it looks like   ,
 from which we may conclude that   .
Hopefully, this second equation will be easier to solve.

     

     

     

     

        is the solution.


4]
     Solve the exponential equation

     

SOLUTION

Factor the equation.

     
By the Zero Product Theorem, we set each factor equal to zero if possible
and solve the resulting equations.

       always, so obviously we can not set it equal to zero.

     

     

The solutions are      and   .




                                                                    top



© edmond 2003