To factor an expression means to rewrite the expression as a product.
If we are asked to factor the number
,
we can write it as 
,
,or
. These would
be correct factorizations. If we wrote
, the
equation would be true but it would not be factorization of
because we have used the operation of addition, not multiplication.To factor almost always will mean to factor an expression completely, that is, to keep
on factoring until we can not factor the subsequent expressions any further.
Factoring
completely,
we write
Although we may start a factoring in several different ways, if we factor the expression
completely, we will always get, except for the order of the factors, the same factorization.
For the case of numbers in our arithmetic, this fact is called
the Fundamental Theorem of Arithmetic.
There are many methods for factoring polynomials.
Factoring by Grouping
When a polynomial has four terms, first try to factor it by the method of grouping.
Here is the idea of the method:
Factor
.Factor something out of the first two terms, then try to factor something appropriate
out of the last two terms, so then the entire expression can be rewritten as a product.
is a factor common to both terms, so we can factor it out of the whole expression
.Always check whether the factoring is correct by doing the indicated multiplication
and see if we get the original expression.
See Examples 2 - 4, pages 25 - 27.
Factoring Second-Degree Polynomials
To motivate this method, let us try to factor
.If the trinomial can be factored, the factoring must look like
.Doing the indicated multiplication and combining like terms,
.Comparing this result with our problem,
,we see that we can do the factoring if we can find two numbers
and 
such that the sum
and the product 
.The numbers
and
work, so
.Note, however, that this method of factoring works only when the number in form
of the squared term is
;
if not, then we need need to look at more combinations of numbers in order to get the correct combination of numbers that will factor the problem.
This leads us to the next case:
Factoring
The method is best illustrated by doing an example.
Factor
.Accounting for the end terms
and 
is always
easy for this type of problem.For example, if we write
as
an attempt at factoring, we get the end terms
and 
,but the middle term in the product is
which is not
,so our attempted factoring is not correct.
To get the correct factoring, essentially we have to proceed by trial and error
until we happen on the right combination of numbers that gives us the answer.
By the distributive law,
.See Example 5, pages 27 - 28.
Special Factoring Identities
The identities we learned earlier for the square of a sum, square of a difference,
and the difference of two squares, that we used to perform multiplications can be
read in the opposite direction to do factoring problems.
To this list we can add the following identities for the sum and difference of two cubes
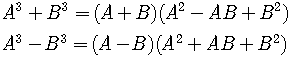
These can be proved by multiplying out the factors on the right side,
or by working on the left side, algebraically playing with the terms until
we get the right side of the identity. Let's do this for the second identity:
.Note that the middle terms just add up to zero.
Now, by grouping, appropriately factor the first two terms and the last two terms,
,using the identity for the difference of two squares.
Now factor out the
,
,which is what we wanted to prove!
See Examples 6 - 7, pages 29 -31.
top
next Rational Expressions: Basic Operations