Quadratic
Equations
Definition
A quadratic equation written so it looks like

is said to be in standard form.
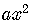 Is the quadratic term.
Is the quadratic term.
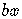 Is the linear term.
Is the linear term.
 Is the constant term.
Is the constant term.
There are several ways to solve a quadratic equation.
Factoring
If the equation written in standard form can be easily factored,
then this is the easiest method.
For example,
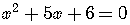
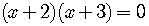 .
.
Now invoke the Zero Product Property:
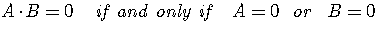 .
.
A product can be equal to zero only when at least one of its factors is equal
to zero.
A multiplication of non-zero numbers can never be equal to zero.


We have replaced one quadratic equation by two simple linear equations
which we know how to solve.
The solution are
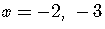 .
.
Note that quadratic equations always have exactly two solutions.
See Example 1, pages 131 - 132.
Square Root
A quadratic equation easily can be solved if it in of the form
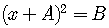 .
.
Just take the square root of both sides.
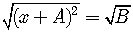

So
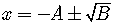 .
.
See Example 2, page 133.
Completing the Square
Case 1) The coefficient of the quadratic term
is 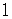 .
.
The idea of this method is based on the preceding.
If a quadratic equation can be rewritten as
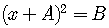 ,
,
then its solution is easy. Let us illustrate the method with an example.
Solve
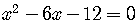 .
.
The coefficient of the quadratic term is 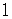 .
.
First, transpose the constant term to the right side, to get it out the way.

Now we want to find a number to add to both sides of the equation
so that the left becomes a perfect square.
That is, so the left side looks like
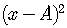 .
.

Let us motivate how we find the number.
Look at the expansion of
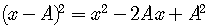 .
.
We can rewrite the constant
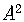
in terms of the coefficient of 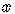 ,
namely,
,
namely,  ,
as
,
as
 .
.
In other words, take one-half the coefficient of the linear term, 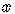 ,
,
and square it.
The square is the number to add to both sides of our problem equation
so that the left side is a perfect square.

and
 ,
,
so
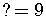
is the number to add to both sides of the equation.

The left side is now a perfect square.

Put 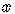 and the
and the 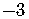 inside the parentheses as
inside the parentheses as 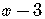 ,
so
,
so
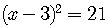 .
.
To convince ourselves that this really works, multiply out the left side,
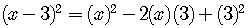
using the identity for the square of difference
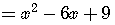 .
.
It works !
To finish the problem, take the square root of both sides of the equation.

Don't forget the "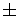 " sign,
otherwise we will get only one solution,
" sign,
otherwise we will get only one solution,
whereas there are two solutions to the equation.
Case 2) The coefficient is the quadratic is
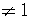 .
.
Divide the equation by the coefficient.
We are back to Case 1).
Solve
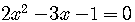 .
.
The coefficient is the quadratic is is 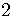 .
.
Divide the equation by 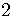 or, equivalently, multiply the equation by
or, equivalently, multiply the equation by 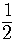 .
.


Now finish the problem.
The solution is
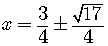 .
.
See Example 4, pages 135 - 136.
The Quadratic Formula
Look at the general quadratic equation in standard form
 .
.
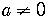 can be any number,
so first we need to divide the equation by
can be any number,
so first we need to divide the equation by 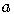 .
.
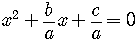
Applying the process of completing the squares, exactly as in the
above examples, we get the quadratic formula,
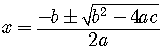 .
.
Caution: To apply the quadratic formula correctly, the quadratic equation
must be written in standard form.
Solve
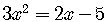 .
.
First, put it in standard form.
One of the sides of the equation must be 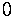 .
.
Which side does not matter. Let's put everything on the left side,
 .
.
Here,
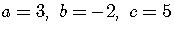 .
.
If we put everything on the right side,
 .
.
Here,
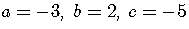 .
.
Which set is the right one to use in the quadratic formula?
The answer is that both sets of numbers are good.
Either set will give the correct solution to the equation.
See Examples 5 - 6, pages 137 - 138.
Look at the expression under the square root of the quadratic formula.
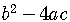
is called the Discriminant.
It can give us qualitative information about the roots of the equation.
Assume that the coefficients of the equation are real numbers.
If
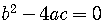 ,
,
there are two equal real roots.
For example,
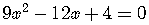 .
.
If
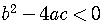 ,
,
the square root of a negative number is an imaginary number,
so the roots are two complex numbers. The roots are complex
conjugates of each other.
For example,
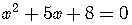 .
.
If
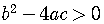 ,
,
there are two distinct real roots.
For example,
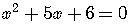 .
.
See Example on page 138.
top
next Equations
Reducible to Quadratic Form