Definition
A function is a correspondence between two sets of elements
such that to each element in the first set there corresponds one
and only one element in the second set.
The first set is called the domain of the function.
The set of all corresponding elements in the second set
is called the range of the function.
For us the domain and the range of a function will, usually, be sets of real numbers.
See the Tables on page 208 and Example 1 on page 209.
Functions Defined by Equations
Read in the usual way, regarding
and
defines
the equation gives out only one corresponding value for
For example, to the value
only the value
Let us see if the equation defines
In other words, given one value for
do we get just one corresponding value for
Let
One
Conclusion: The equation does not define
See Example 2, page 211.
The graph of an equation makes it easy to determine whether the equation
defines a function or not.
(a) (b)
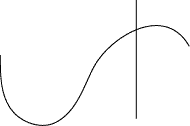
Vertical Line Test for a Function
The equation defines a function if each vertical line in the rectangular
coordinate system cuts the graph of the equation in at most one point.
See figure (a) above.
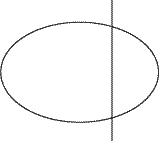
If any vertical line cuts the graph of the equation in two or more points,
the equation does does not define a function.
See figure (b) above.
See Figure 1 on page 212.
Finding the Domain of a Function
The domain of a function is the set of all real numbers
that are meaningful replacements for
Example
So the domain is the set
Example
We exclude negative values of
in the range of a function.
So the domain is the set
Example
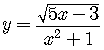
The denominator
on the possible domain of the function.
The numerator, however, contains a square root, so the radicand must be
greater than or equal to zero in order for the square root to be a real number,
The domain is the set
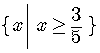 .
.See Example 3, page 213, and Example 5, page 216.
Functional Notation
The equation
as
Typical problems associated with using functional notation are:
Example
Find
wherever
Usually, there is no problem evaluating the function when a number
replaces the variable, as in the example above.
Example
Find
A problem like this, with another expression involving the independent variable,
often causes some confusion.
To avoid this confusion, when given the definition of
immediately replace the independent variable
in order to avoid being confused by the use of a particular symbol
for the independent variable,
Wherever
To find
appears in the above equation,
Do the algebra,
See Example 4, page 215, and Examples 6 - 7, pages 217 - 218.
top
next Graphing Functions