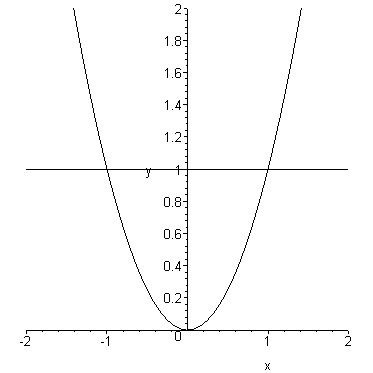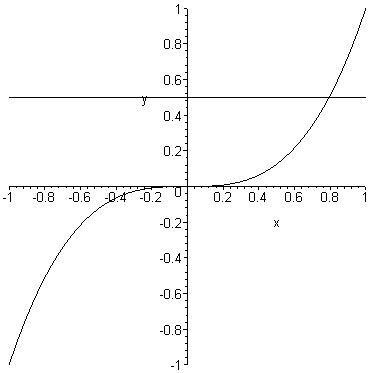Inverse
Functions
Recall the definition of when a relation, or equation, defines a function:
A relation between two variables - say, 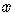 and
and 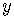 - defines
- defines 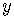 as
as
a function of 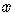 ,
if to each value of
,
if to each value of 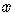 there corresponds at most
there corresponds at most
one value of 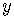 .
.
For example, the following equation defines 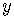 as a function of
as a function of 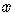
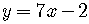 ,
,
because to a given value of  ,
we can calculate only one value of
,
we can calculate only one value of 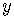 .
.
Given 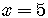 ,
then
,
then 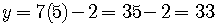 .
.
The equation 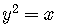 does not define
does not define 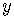 as a function of
as a function of 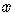 ,
,
because to a given value of 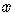 ,
we can calculate not one but two values of
,
we can calculate not one but two values of 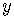 .
.
Given 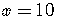 ,
,
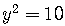
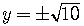 .
.
Definition of One-to-One Function
A function is one-to-one if to each value of 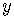 in its range,
in its range,
there corresponds only one value of 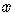 in its domain.
in its domain.
In other words, if a function is one-to-one, then the relation that we get
when we solve the relation for for 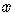 ,
,
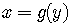
is also a function.
To a given value of 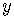 ,
there corresponds only one value of
,
there corresponds only one value of 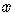 .
.
The relation 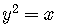 is not one-to-one.
is not one-to-one.
See Example 1, page 259 - 260.
Often it is not easy to determine if a function is one-to-one.
For example, it is not easy to solve the equation
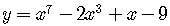
for  in
order to see whether one value of
in
order to see whether one value of 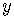 determines only one value of
determines only one value of  .
.
But if we know the graph of a function, we need only apply the
Horizontal Line Test.
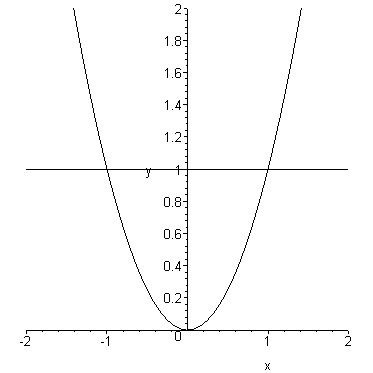
not
one-to-one
If a horizontal line intersects the graph of a function in more than one point,
then the function is not one-to-one.
If each horizontal line intersects the graph of a function in at most one point,
then the function is one-to-one.
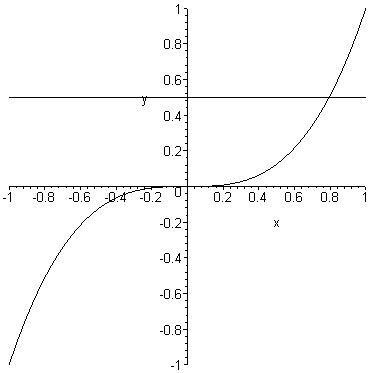
one-to-one
See Figure 1 - 2, pages 260 -261.
Finding the Inverse Function
If 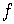 is a one-to-one function, then it has an inverse function denoted by
is a one-to-one function, then it has an inverse function denoted by 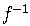 .
.
If 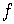 is not one-to-one,
it does not have an inverse function.
is not one-to-one,
it does not have an inverse function.
If the function 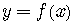 is one-to-one, then we can solve the equation for
is one-to-one, then we can solve the equation for 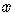
to get an equation expressing 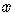 in terms of
in terms of 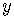 ;
this equation expresses
;
this equation expresses 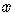 as
as
a function of 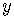 and this function of
and this function of 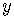 is called the inverse function of
is called the inverse function of 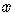 ,
,
denoted by
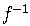 .
.
A little confusing, yes.
Here is an example illustrating the terminology and the notational conventions
employed.
Find the inverse function for 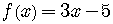 .
.
Recall that the equation can also be written as 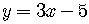 .
.
Recall that 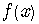 and
and 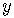 both represent the ordinate of the same point
both represent the ordinate of the same point
on the graph. The graph of 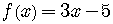 and the graph of
and the graph of 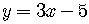
are the same.
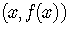 and
and 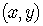 both name the same point on the graph.
both name the same point on the graph.
Okay, here is the process:
Use
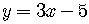 .
.
Solve this equation for 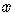 .
.
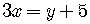
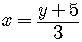
Note that given one value for 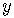 ,
this equation gives only one value for
,
this equation gives only one value for 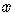 .
.
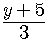 is already the inverse function we are looking for.
is already the inverse function we are looking for.
The convention, however, is to use the 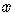 variable to write the inverse function.
variable to write the inverse function.
Simply interchange the 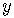 and the
and the 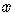 ,
,
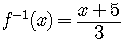 .
.
For inverse functions, 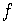 and
and 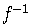 ,
it is true that
,
it is true that
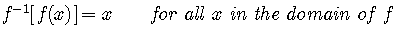
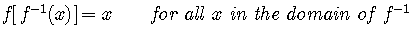
See Examples 2 - 3, pages 266 - 270.
top
next Polynomial
Functions and Graphs
Module
4