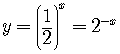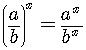Exponential
Functions
Functions of the form
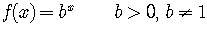
are called exponential functions.
The domain of 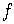 is the set of all real numbers.
is the set of all real numbers.
The range of 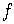 is the set of all positive numbers.
is the set of all positive numbers.
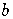 is called the base.
is called the base.
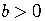 is required in order to avoid imaginary numbers.
is required in order to avoid imaginary numbers.
For
example, 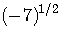 is imaginary.
is imaginary.
Basic Exponential Graphs
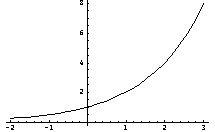
The graph
of 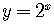
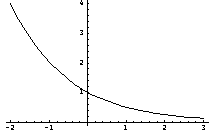
The graph
of 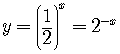
These two graphs illustrate the basic shapes.
Basic properties
All graphs
1) go through the (0,1) 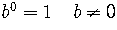
2) are continuous, no holes, no jumps
3) the x-axis is a horizontal asymptote
4) if 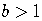 , the graph always goes up as a point
, the graph always goes up as a point
on the graph moves to the right
5) if 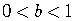 ,
the graph always goes down as
,
the graph always goes down as
a point on the graph moves to the right
6) the function 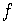 is one-to-one.
is one-to-one.
Property 6 means that the exponential function has an inverse
that is also a function.
We can solve the equation 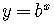 for
for 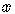 ,
,
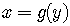 .
.
This inverse function 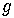 is called the logarithmic function.
is called the logarithmic function.
We soon will study it.
See Example 1, page 357.
Exponential Function Properties
The functions obey all the basic laws for exponents.
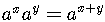
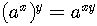
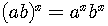
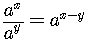
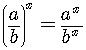
In addition,
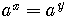 if and only if f
if and only if f 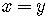 .
.
If 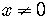 , then
, then
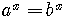 if and only
if
if and only
if 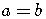 .
.
These last two properties are useful in solving exponential equations.
See Example 2, page 358.
Applications of Exponential Functions
Population growth, radioactive decay, compound interest.
See Examples 3 - 5, pages 359 - 363.
top
next The
Exponential Function with Base e