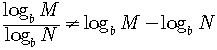Logarithmic
Functions
Definition
For 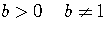 ,
,
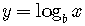 is equivalent
to
is equivalent
to 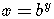 .
.
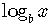 is read "the logarithm
of
is read "the logarithm
of 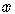 to the base
to the base
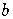 ".
".
Note that the values of the logarithm are exponents.
The logarithm of 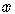 to the base
to the base 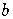 is
the power
is
the power
to which 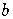 must be
raised in order to get
must be
raised in order to get 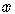 .
.
Example
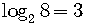 because
because 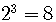 .
.
The logarithmic function and the exponential functions are inverse functions of
each other.
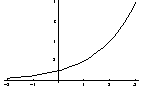
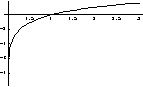
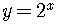
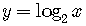
For 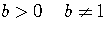 and
and 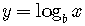 ,
,
the domain of the function is the set of all positive real number,
the range of the function is the set of all real numbers, positive,
negative, and zero.
Look at the graph of 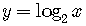 .
.
It is typical.
See Examples 1 - 3, pages 378 - 379.
Properties of the Logarithm
For 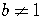 ,
,
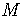 ,
, 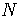 positive real numbers, and
positive real numbers, and 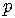 ,
,
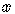 real numbers,
real numbers,
1)
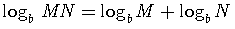
(The
log of a product is equal to the sum of the logs.)
2)
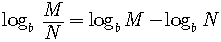
(The
log of a quotient is equal to the difference of the logs.)
3)
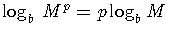
(The
log of a power is equal to the power times the log.)
4)
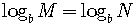 if and only if
if and only if 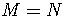
5)
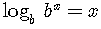
6)
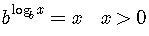
7)
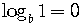
8)
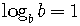
Let us prove Property 1:
Let 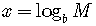 and
and 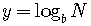 .
.
By definition, these are equivalent to 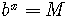 and
and 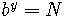 .
.
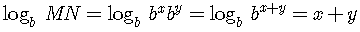
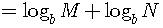
The other properties are proven in the same way.
Property 4 is true because the logarithmic function is one-to-one.
See Examples 4 - 7, pages 381 - 383.
CAUTION
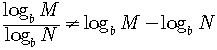
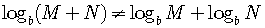
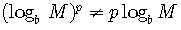
top
next Common
and Natural Logarithms