Multiplication Principle, Permutations and Combinations
Here we will study the theory of counting, called combinatorics.
We want to determine the number of ways in which certain sets
of objects can be arranged, combined, or chosen.

Look at the problem:
How many 3-letter code symbols can be formed
with the letters A, B, C, D. and E
without repetition, that is, without allowing a letter to be repeated?

Think of putting the letters into three slots.
There are 5 letters in all. In the first slot, we can put any one
of the 5 letters, so in the first slot we have 5 possible choices.
Once that choice is made, the second slot can be filled with
any one of the 4 remaining letters (remember, no repetition
of letters allowed); that is, in the second slot there are 4
possible choices. Similarly, in the third slot, there are 3
possible choices. So the the total number of 3-letter
codes that can be formed is the product
5 times 4 times 3.
           5  x   4  x  3
     


This problem illustrates the application of the
Fundamental Counting Principle, also know as the
Multiplication Principle
1)
If two operations    and    are performed in order,
with    possible outcomes for the first operation and 
possible outcomes for the second operation, then there are
                
possible combined outcomes of  the first operation followed
by the second operation.
2)
Generally, if    operations   ,   , . . .,   
are performed in order, with possible number of
outcomes   ,   , ...,   , respectively,
then there are
          
possible combined outcomes of the operations performed
in the given order

See Examples 1 - 3, page 833 - 835.


The solution of the problem above is an example of
Permutations of    Objects Taken    at a Time
A permutation of a set of   objects is an ordered arrangement
of all    objects, without repetition.
The permutation of    objects taken   at a time is represented
by the symbol   ,
     
and when   ,

     

The solution of the 3-letter code problem above can be given
as the permutation of 5 objects (the letters A, B, C, D, and E)
taken 3 at a time, or  .

Another form of the formula for can be obtained as follows:


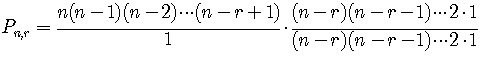
On the right the second factor is . It is just     .

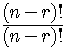So
  

See Examples 4 - 5, pages 838 -839.


Combinations
When the order in which we arrange objects does not matter,
we are dealing with a problem in combinations.

Example
How many committees can be formed from a group of 5 governors
and 7 senators if each committee contains 3 governors and 4 senators?

The order in which we select the 3 governors from the group of  7
governors does not matter. Whether we select David, Bill, and
George OR Bill, David, and George OR George, David, and Bill
OR . . . does not matter, we have chosen the same 3 men.
So this is a problem in combinations.

The number of ways in we can select 3 governors from a group of 5
governors is the number of combinations of 5 objects taken 3 at a time,
symbolically
      .

Similarly, the number of ways in we can select 4 senators from a group
of 7 senators is the number of combinations of 7 objects taken 4 at a time,
symbolically
      .

By the Multiplication Principle, the number of possible committees is the
product
       .


Combination of Objects Taken at a Time

     


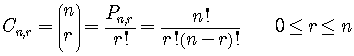
Now we can complete the solution to the committee problem above.

The number of possible committees is
     

           

           


See Examples 6 - 9, pages 840 - 843.


                        top
                                End of Module 6