The Variable-Depth Formula
Fluid Forces
The pressure of water against a point on the surface of a damn depends
only on how far below the surface the point is and not on how much the
surface of the damn happens to be tilted at that point. The pressure in
pounds per square foot at a point
The number
Damns are designed to be thicker at bottom than at the top because the water
pressure against them increases with the depth.
The Pressure-Depth Formula:
Generally, in a fluid that is not in motion, the pressure
is the fluid's weight-density
Fluid Force on a Constant-Depth Surface
If the container of fluid has a flat horizontal base, then the total force
by the fluid on the base is force per unit area times area, or pressure times area:
On the vertical surface of the container, the pressure at a point will depend on the
depth of the point below the surface. Since the pressure will be different at different
depths, the total total force will not be given by the above constant-depth formula.
By dividing the vertical surface into many narrow bands or strips, we can make a
Riemann sum whose limit is the fluid force against the side of the submerged vertical
surface.
See Example 1, pages 433 - 434.
The Variable-Depth Formula
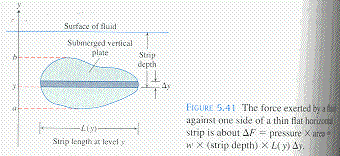
Suppose a plate that is submerged vertically in fluid of weight-density
runs from
Let
along the surface of the plate at level
Then the force exerted by the fluid against one side of the plate is
This is the integral for fluid force against a vertical flat plate.
See Examples 2 - 3, page 435 - 436
next Moments and Centers of Mass
Top