The Disk Method
Washer Cross Sections
Volumes by Slicing and Rotation About an Axis
Volume of a Solid
If the area of a cross-section of a solid is
,then the volume of the solid from
to 
is given
by
.See Examples 1 - 3, pages 394-396.
Solids of Revolution: Circular Cross Sections. The Disk Method.
If we revolve a plane region about an axis, a solid of revolution is generated.
When the cross-sections of the solid are circles perpendicular to the axis of
revolution, then the area of the cross-section is given by
,where
is the radius
of the circle.The volume of the solid of revolution is given by
.See Examples 4 - 7, pages 396 - 398.
Washer Cross Sections
If the planar region that is revolved about the axis of revolution is away
from the axis of revolution, then the solid generated has a hole in it.
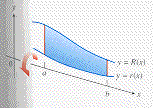
The planar region does not intersect the x-axis.
The cross-sections look like washers.
The outer radius of the washer is
.The inner radius of the washer is
.
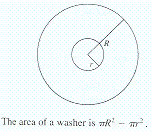
The area of the washer is the area of the big circle minus the area of the
smaller circle:
.See Example 8 - 9, pages 399 - 401.
next Modeling Volume Using Cylindrical Shells
Top