Infinite Limits of Integration
The Integral

Integrals with Infinite Discontinuities
Tests for Convergence and Divergence
Computer Algebra Systems

Improper Integrals
Until now, our definite integrals had the two properties:
     the domain of integration from was finite
     on the domain, the values of the integrand were finite.

Improper integrals occur when
      the domain is infinite
      the integrand becomes infinite

We define the value of an improper integrals as the limit, if it exists,
of a proper integral.
Definition of Integrals with Infinite Integration Limits
If
 
 is continuous in the given domain:

domain  , 
                         then      

domain ,
                        then     

domain ,
                        then     ,
where    is any real number.
The choice of    is not important.
Any convenient choice will do. If the limits exist, any value of   
will give the same value of the improper integral.
Often, the choice    simplifies the algebra in the evaluation
of the definite integrals.
If the limits on the right side of the definition exist,
then the improper integral is said to converge.
If the limits do not exist, then the improper integral is said to diverge.

See Examples 1 - 2, pages 588 - 589.


The Integral
For what value of    does the integral converge?
When it converges, what is the value of the integral?
If  

,
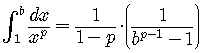so

                      The improper integral converges.
                                 The improper integral diverges.

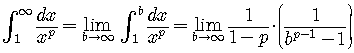
If



                  The improper integral diverges.

See Example 3, pages 589 - 590.


Integrands with Infinite Discontinuities
Graphically, at an infinite discontinuity the function has a vertical asymptote.
When the integrand tends to infinity at a limit of integration
or at some point between the limits of integration, the following definition applies.

Definition of Improper Integrals with Infinite Discontinuities:
If
   is continuous on  ,
then
.
In the above, the discontinuity is assumed to be at  .

If
  is continuous on  ,
then
.
In the above, the discontinuity is assumed to be at .

If
  is continuous on   ,
then
.
In the above, the discontinuity is assumed to be at  .

See Examples 4 - 7, pages 591 - 593.

Tests for Convergence and Divergence
Before going through the work of evaluating an improper integral,
often it's a good idea first to test whether it converges or diverges.
If it diverges, we're done.
If it converges, then we can try numerical methods if necessary to
evaluate the improper integral.

See Example 8, pages 593 - 594.


Direct Comparison Test
Let
  and   be continuous 
and
   for all   .
Then
  converges if      converges.
 diverges if       diverges.

See Example 9, page 594.


Limit Comparison Test
If the positive functions
  and    are continuous on 
                              and if
,

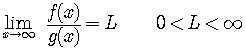then

  and   
both converge or both diverge.

Both integrals converging does not mean that they have the same value.

See Examples 10 - 11, pages 595 - 596.


Computer Algebra Systems
Improper integrals may be evaluated using Maple and Mathematica.

See Example 12, page 596.

                End  of  Modules
                      Top