General Description of the Method
The "Heaviside" Cover-up" Method for Linear Factors
Other Ways to Determine the Coefficients
Partial Fractions
As it stands, the integral
is not directly workable.
At this point, the integrand is a bit too complicated for us.
But if we can break it up into other fractions whose integrals
we know, then we can solve it.
In other words, if we can write
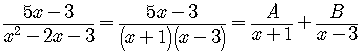 ,
,then we can solve the problem because we know how to integrate
each of the fractions on the right side of the equation.
We need only to determine the values of the constants
The method of breaking up a big fraction into a sum of simpler, basic
fractions each of which we can integrate is called the
method of partial fractions.
It is always possible to do this.
Example 1, page 556, shows that
General Description of the Method
Using a Repeated Linear factor
See Examples 2 - 3, pages 557 - 558.
Integrating an Improper Fraction
See Example 4, page 558
Integrating with an Irreducible Quadratic Factor in the Denominator
See Examples 5 - 6, pages 558 - 559.
The Heaviside "Cover-up" Method for Linear factors
When the denominator of a proper fraction is made up of a product of
linear factors, each raised to the first power, this method is a fast way of
determining the constant numerators of the partial fractions.
See Example 7 - 8, pages 560 - 562.
Other Ways to Determine the Coefficients
Differentiation . . . see Example 9, page 562 - 563.
Assigning Numerical values to x . . . see Example 10, page 563.
next Trigonometric Substitutions
Top