Rules for Working with Exponents
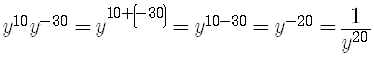
	The Multiply Rule                           When you multiply powers to the same base, you add the exponents. Examples are                          Negative Exponents                           Negative exponents are defined as reciprocals. so             The point of the above example is that the exponent rules apply no matter what the exponents are. Whether the exponents are simply numbers or complicated expressions with symbols and variables in them, the exponent rules apply, they are true. When you multiply powers to the same base, you add the exponents. Period. No exceptions!                             The Divide Rule                            When you divide powers to the same base, you subtract the exponents. You always do the exponent on the top minus the exponent on the bottom. Always!                           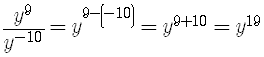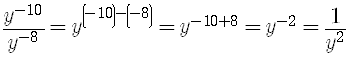Examples are                   When you divide powers to the same base, you subtract the exponents. How big the exponents are is not important, you always do the exponent on the top (the numerator of the fraction) minus the exponent on the bottom (the denominator of the fraction). Again, Look at the examples above, that is what you always do in each example.                     The Power Rule                  When you raise a power to a power   m   you multiply the exponents, so you get for the answer. 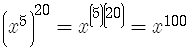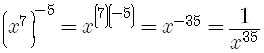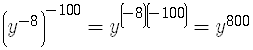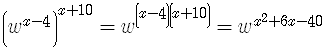Examples are                                        The Product Raised to a Power Rule                           When you raise a product to a power, you raise each factor of the product to that power. Examples are       Everything thing that is multiplied is a factor., including the number which is multiplying so must also be raised to the 2nd power just like the other factors in the product. To finish the problem, use the Power Rule.                                                  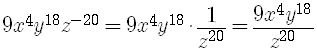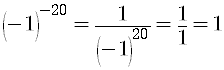Write the final answer using positive exponents only, so                Here's another example       Remember that       So is the final answer.                     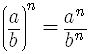The Fraction Raised to a Power Rule                                      When you raise a fraction to a power, you raise both the numerator and the denominator to that power. 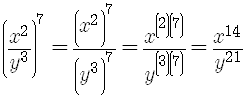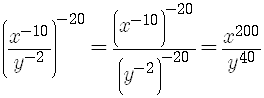Examples are             Remember that the exponent rules apply no matter what the exponents are, whether the exponents are numbers or symbols.                                                                             top © edmond 2001