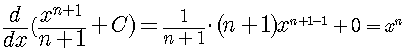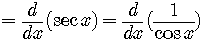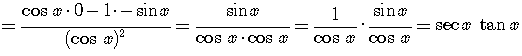Indefinite Integral
Checking
Indefinite Integral Formulas
Indefinite Integrals
One interpretation of the derivative of a function is that the drivative gives you the slope
of the graph of the function. Given a function, you can find the slope at a specific point
of the graph of the function by finding the value of the derivative of the function at that
specific point.
For example, if the function is
then to find the slope of the graph of the function at the point
,
you find thederivative of the function
and substitute
.At that point the slope of the graph is
The problem going in the opposite direction is to find the function itself when you
are first given the derivative of the function.
For this example, the problem would be to find
when you are given that.The solution of this problem brings in the integral calculus.
The monomial
is simple enough so it is not so hard to determine that 
works for a solution.
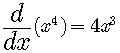
So
is a solution to the problem.But
, 
, and 
all work too, as you can verify by taking their drivative.
Each of these functions is called an antiderivative of
.In fact, any combination of the form
, where C is a constant, works.
The general form
is called the indefinite integral of .The notation is
is called the constant
of integration.In general,
where
.Checking an Indefinite Integral
is needed because when 
,
the denominator become 
.
. 
