4 )
Express
as a single radical
ANSWER
Expressing as a single
radical means you must re-write
as
some root of some number,
that is,
You must find out
what numbers to put in for the "?".
Let's do it!!
Re-write the roots
using rational exponents
so
The denominator of
the fraction tells you the root, so if we convert the exponents 1/2
and 1/9
into equivalent
fractions with the same denominator, then we will the single radical that
we want,
because the denominator
tells you what the radical is.
In this case, you
use the lowest common denominator, the LCD, of the fractions 1/2 and 1/9,
which is 2 times 9
or 18.
so
Then you use the exponent
rule that says when you raise a product to a power
you must raise each
factor of the product to that power
so
Now you can re-write
the rational exponent 1/18 as a radical, namely,
the eighteenth root, so
is
the answer, because you have rewritten
as
a single radical, namely, 
5)
By completing the squares, solve the quadratic equation
ANSWER
The goal of the process
of completing the squares is to re-write the equation so that it looks
like
which can be solved
for 
very quickly by taking the square root of both sides
and then adding
to both sides of the equation in order to get
alone,
so
Remember
that completing the squares works only
when the number in front
of the 
is 1 ,
so you must first
divide both sides of the problem equation by 2 .
Dividing both sides
of the equation by 2 is the same as multiplying
both sides of the
equation by 1/2
or
Now add
to both sides of the equation to get
You need to add some
number to both sides of the equation so that the left side
becomes a perfect
square, in other words, so that
the left side can
be rewritten as
This is where the
process of completing the squares really comes in.
You take 1/2 of the
number in front of the
and square it
and 
so
is
what you add to both sides of the equation so that the left side of the
equation
becomes a perfect
square
The left side now
can be rewritten as
Doing the arithmetic
on the right side of the equation, you must add the two fractions,
using the lowest common
denominator which is 16,
So the above equation
becomes
Now all you need to
do is to take the square root of both sides of the equation
Work out the squares
roots and simplify, and remember that a quadratic equation
always has two solutions
so you must put in the 
signs in order to get the two solutions
To finish the problem
and solve the equation for 
, you must get
alone
on the left side of
the equation, so you need to
add
to
both sides of the equation
So
When you use the
in
, you get
When you use the
in
,
you get
Now you have the two
solutions to the problem
and
Using set notation,
you also can say that the solution set is the set
6)
Find the center and the radius of the circle
ANSWER
You must re-write
the given equation in the standard form of the equation of the circle
where the
h and the k in the parenthesis are
the coordinates of the center of the circle
and the radius of
the circle is r.
For
example, if the equation already is given in standard form, say,
then the center of
the circle is given by 
and the radius of the circle is 
.
The way to re-write
the given equation in order to put it in standard form is to do
completing the squares
on the 
and the 
.
Okay, do it now!
First, group all the
and
all the
, and get rid of the 
by adding 
to both sides of the
equation
or
Now complete the squares
for the
and the
inside the parenthesis.
You remember the process,
take 1/2 of the number in front of the linear term (the linear term
is the term that is
raised to the first power), square it, then add it inside the parenthesis
and add it
to the other side
of the equation.
you must do the same
thing to both sides of the equation to keep the equation in balance, so
to speak
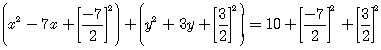
Simplifying this,
you get
Now, on the left side
of the equation you get two perfect squares
Comparing the equation
to the standard form of the equation of a circle, you can read off
the center of the
circle and the radius of the circle for our problem.
The center is
.
The
radius is 
.
or,
equivalently, if you rationalize the denominator, the radius is
top
Review
1 Problems Only
© edmond 2001