Review 2 Problems Only Algebra B
SOLUTIONS
1  2    3a  3b   3c  


     1] Express as a single logarithm with a coefficient of 1.

               

     SOLUTION

     Use the laws for working with logarithms.

          (i)   Product Law
               The logarithm of a product is the equal to the sum of the logarithms.

          (ii) 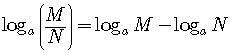  Quotient Law
               The logarithm of a quotient is equal to the difference of the logarithms.

          (iii)   Power Law
               The logarithm of a power is equal to the power times the logarithm.


     In this problem all three laws are involved - products, quotients, and powers.

     Also, we must re-write the square roots as powers (using fractional exponents)
     in order to be able to use the power rule (iii).

             

          


     


          


         

     Now drop the parentheses.


        

     Combine like terms.

        

        


        

     Since the problem was given in terms of radicals, let's write the final answer
     likewise in terms of radicals.

        



     2] Express as a single logarithm with a coefficient of 1.

             


     SOLUTION

     Here the logarithms are all strung out and the problem is to put them together
     so that the final answer will look like

              .

     Use the three laws (i) - (iii). And, of course, the laws for working with exponents.


          

         


     Now combine the logarithms. Differences are replaced by quotients and sums
     are replaced by products.

         

                This is the final answer.

     We have done it!
     We have found that     .



     3] Expand in terms of simpler logarithmic forms.

          (a)
                    


     SOLUTION
     Again, re-write the radical in terms of fractional exponents
     so we can use the power rule (iii).

     

          

         

         

         


     Always simply as much as we can. Remember that  .
     So the final answer is

         


     (b)
               


     SOLUTION

          
     This is as far as we can go. There is no law for re-writing the logarithm of a sum!
          The only laws for working with logarithms are the three laws (i) - (iii) listed above .


     WARNING!
          

          


     (c)
               


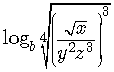
     SOLUTION

     

     

    

    


                    is the final answer!


                                                                                             top

                                                                              Review 2 Problems Only


     © edmond 2002